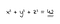
Dette fordi, den 6. September 2019, annonserte et team ledet av forskere ved University Of Bristol og MIT at de hadde oppdaget den endelige løsningen på det såkalte» summene av tre kuber » – problemet, som ber om heltallsløsninger til ligningen x3 + y3 + z3 = k for verdier av k mellom 1 og 100. Siden formuleringen i 1954 ved University Of Cambridge, frem til 2016, hadde hver løsning blitt funnet bortsett fra to, for k=33 og k = 42. I Mars i år, matematiker Andrew R. Booker i et papir publisert på arXiv.org annonserte at han hadde funnet den riktige løsningen for k = 33 ved hjelp av uker med beregningstid på Bristols supercomputer. Hans løsning, presentert i papiret «Cracking problemet med 33» er:

så, bare en uke eller så siden, igjen nyheten brøt: k=42 hadde blitt oppdaget, igjen av booker sammen med en annen andrew, andrew sutherland ved mit, ved hjelp av mengden hentet såkalte veldedighet motor. Deres svar er:

for verdier av k mellom 1 og 1000, finnes det fortsatt løsninger for heltallene 114, 165, 390, 579, 627, 633, 732, 906, 921 og 975.
summene av three cubes problem er et eksempel på et problem som ber om løsninger På En Diofantinligning, som kan defineres som:
Definition
A Diophantine equation is an algebraic equation with several unknowns and integer coefficients.
Det Vil Si At Diofantinligninger er ligninger med flere ukjente variabler (x, y, z,..) hvis løsninger (=0) bare vises når koeffisientene til ligningen (a, b, c,…) er heltall ( … ,-2, -1, 0, 1, 2, … ).
Den Lineære Diofantinligningen
en lineær Diofantinligning er en ligning av første grad hvis løsninger er begrenset til heltall. Den prototypiske lineære diofantinske ligningen er:
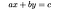
hvor a, b og c er heltallskoeffisienter og x og y er variabler. Typiske lineære diofantinproblemer involverer derfor hele mengder, som f.eks. Brilliant.org, 2019):
How many ways are there to make $2.00 from only nickels and quarters?
løsningene på problemet er funnet ved å tildele variabler til antall nickels (x) og antall kvartaler (y). Vi vet at $2 er 200 cent (c), og at en nikkel er verdt 5 cent (a) og en kvart 25 cent (b). Dermed kommer vi lett til ligningen som angir antall måter vi kan ha $2,00 i nikkel og kvartaler:

Linear Diophantine equations have integer solutions if and only if c is a multiple of the greatest common divisor of a and b.If integers (x, y) constitute a solution to the linear Diophantine equation for given a, b and c, then the other solutions have the form (x + kv, y - ku) where k is an arbitrary integer and u and v are the quotients of a and b (respectively) by the greatest common divisors of a and b.
den største felles divisoren (GCD) av to eller flere heltall, som ikke er alle null, er det største positive heltallet som deler hvert av heltallene. For vårt eksempel ovenfor, kan vi begynne med factoring ut felles divisor 5, skaffe:

den største felles divisoren av a og b, 1 og 5, er 1. Enhver ikke-negativ c er et multiplum av 1. Det er ni slike multipler av 5 som er mindre enn eller lik 40. De er 0, 5, 10, 15, 20, 25, 30, 35, 40. Derfor, det er ni måter å gjøre $2,00 fra nickels og kvartaler. De er:
(0, 8), (5, 7), (10, 6), (15, 5), (20, 4), (25, 3), (30, 2), (35, 1) og (40, 0).prosessen ovenfor er en enkel versjon av Det Som kalles Diofantinanalyse, prosessen som kreves for å finne løsninger På Diofantinligninger. Spørsmålene som vanligvis stilles under slike analyser er:
- Er det noen løsninger?
- Er det noen løsninger utover noen som lett blir funnet ved inspeksjon?
- Er det endelig eller uendelig mange løsninger?
- Kan alle løsninger bli funnet, i teorien?
- Kan man i praksis beregne en fullstendig liste over løsninger?Populære teknikker som brukes til å løse Diofantinske ligninger inkluderer faktornedbrytning, avgrensning av ulikheter, parametrizering, modulær aritmetikk, induksjon, Fermats uendelige nedstigning, reduksjon Til Pell og fortsatte fraksjoner, posisjonstallsystemer og elliptiske kurver (Wikiversity, 2019).
Hardy-Ramanujan-Ligningen
Hardy-Ramanujan-tallet 1729, kjent som et «drosjenummer», er definert som «det minste tallet som kan uttrykkes som summen av to kuber på to forskjellige måter», fra en anekdote av Den Britiske matematikeren G. H. Hardy da han besøkte Indisk matematiker Srinivasa Ramanujan på sykehuset:
«jeg husker en gang å se ham da han var syk På Putney. Jeg hadde ridd i drosje nummer 1729 og bemerket at nummeret virket for meg ganske kjedelig, og at jeg håpet det ikke var et ugunstig tegn. «Nei,» Svarte Ramanujan, » det er et veldig interessant tall ;det er det minste tallet som kan uttrykkes som summen av to kuber på to forskjellige måter.»- G. H. Hardy (1918)
ligningen i hjertet av taxicab tall Er Diofantin, nemlig ligningen:

de to forskjellige måtene 1729 er uttrykkbar som summen av to kuber er 13 + 123 og 93 + 103. Så langt er seks taxicab tall kjent. De er:
Ta(1) = 2
= 1³ + 1³Ta(2) = 1,729
= 1³ + 12³ = 9³ + 10³Ta(3) = 87,539,319
= 167³ + 436³ = 228³ + 423³ = 255³ + 414³Ta(4) = 6,963,472,309,248
= 2421³ + 19083³ = 5436³ + 18948³ = 10200³ + 18072³ = 13322³ + 16630³Ta(5) = 48,988,659,276,962,496
= 38787³ + 365757³ = 107839³ + 362753³ = 205292³ + 342952³ = 221424³ + 336588³ =231518³ + 331954³Ta(6) = 24,153,319,581,254,312,065,344
= 582162³ + 28906206³ = 3064173³ + 28894803³ = 8519281³ + 28657487³ = 16218068³ + 27093208³ = 17492496³ + 26590452³ = 18289922³ + 26224366³Fermats Siste Teorem

den Opprinnelige Setningen av fermats siste teorem
tall som kan uttrykkes som summen av kuber (slik som de fra summen av tre kuber problem og hardy-ramanujan nummer) ble først nevnt i 1657 av bernard fré de bessy, som beskrev det som en eiendommen siterer eksempel på antall 1729 i hans korrespondanser med john wallis Og Pierre De Fermat. Fermats navn siden har blitt noe synonymt med det mer generelle tilfellet av problemet, etter hans 1637 påstand i margen av en kopi Av Diophantus’ Arithmetica at ingen tre positive heltall a, b og c tilfredsstiller Diophantine ligningen
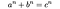
som fermat (in)famously uttalt at han hadde vist seg å være sant for heltallverdier av n større enn 2, men som han ikke kunne inkludere i sine notater i boken fordi marginen var for smal:
Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet - Pierre de Fermat, 1637
Oversatt, hans tekst leser » Det er umulig for en kube å være summen av to kuber, en fjerde kraft å være summen av to fjerde krefter, eller generelt for et hvilket som helst tall som er en kraft større enn den andre til å være summen av to like krefter. Jeg har oppdaget en virkelig fantastisk demonstrasjon av dette forslaget at denne marginen er for smal til å inneholde.»(Nagell, 1951).gjetningen ble berømt endelig bevist etter 358 år i 1994 av engelsk matematiker Andrew Wiles i hans papir Modular elliptic curves og Fermats Siste Teorem publisert i Annals Of Mathematics 141 (3), pp 443-551. Wiles ‘ proof by contradiction, på 129 sider lang, bruker teknikker fra algebraisk geometri og tallteori for å bevise et spesielt tilfelle av modularitetsteoremet for elliptiske kurver, som sammen Med Ribets teorem innebærer sannheten Til Fermats Siste teorem. På grunn av sin omfattende bruk av moderne matematikk, er det sikkert At Wiles ‘ bevis ikke kan være det samme som Hevdes å bli funnet av Fermat-som fortsatt er tapt (og sannsynligvis ikke var et bevis i det hele tatt).
Pythagoreiske tripler
Den kanskje mest kjente diofantinske ligningen av alle er et spesielt tilfelle av ligningen fra Fermats Siste Teorem, men for n=2. Dette er ligningen som hjelper en finne lengden på sidene av en rettvinklet trekant
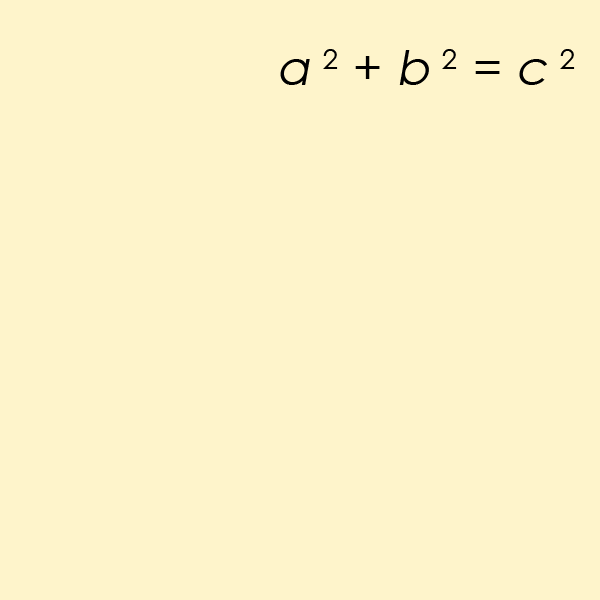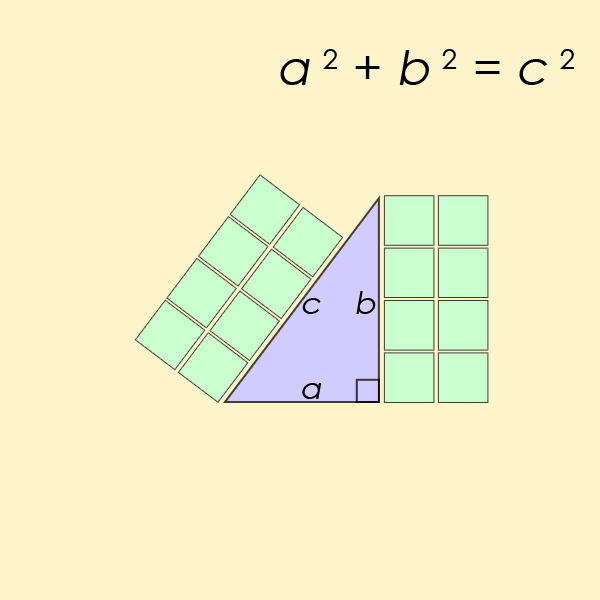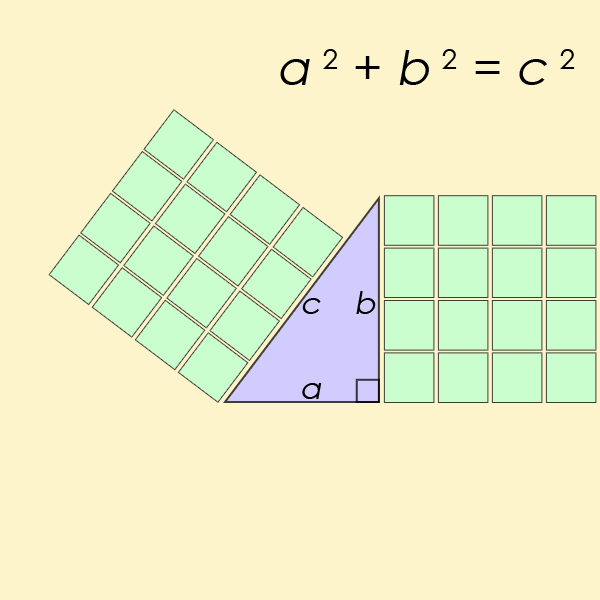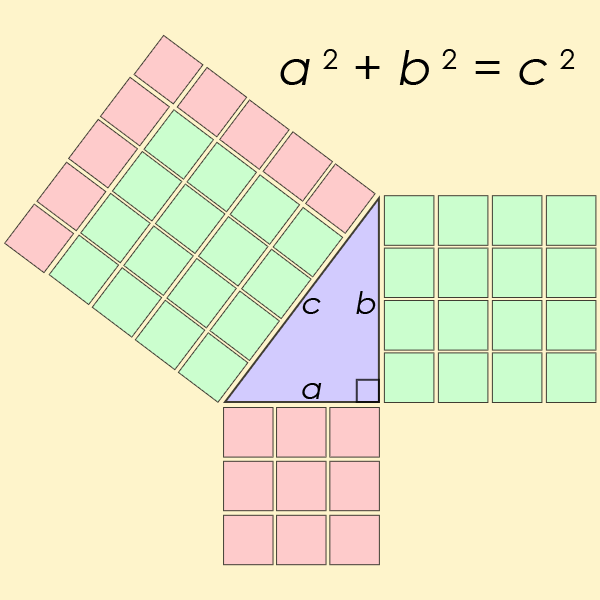
animasjon som demonstrerer den enkleste pythagoranske trippelen, 32 + 42 = 52 (wikipedia, 2019). Pells Ligning
Pells ligning (noen ganger Pell-Fermat-ligningen) er en ligning av følgende form hvor n er et gitt positivt kvadratfritt heltall og heltallsløsninger søkes for x og y:

Ligninger av Formen Av Pells ligning med n = 2 er kjent for å ha blitt studert så tidlig som 400 F. KR. i Både India og Hellas, i tillegg til tilfellet der x2 − 2y2 = -1, på grunn av forbindelsen mellom disse to ligningene til det irrasjonelle tallet som er oppnådd ved å beregne kvadratroten av 2 (hvis x og y er positive heltall som tilfredsstiller denne ligningen, er x/y en tilnærming av √2).
i Kartesiske koordinater har ligningen form av en hyperbel, da løsninger på ligningen oppstår hvor kurven passerer gjennom et punkt hvis x-og y-koordinater er begge heltall, for eksempel x = 1, y = 0 og x = -1, y = 0. Lagrange viste at så lenge n ikke er et perfekt kvadrat, Har Pells ligning uendelig mange forskjellige heltallsløsninger.
Erd@s–Straus Formodning
Erdő-Straus formodning sier at for hvert heltall større enn 2, kan det rasjonelle tallet 4 / n uttrykkes som summen av tre positive enhetsfraksjoner. Det vil si, for hvert heltall n ≥ 2, finnes det positive heltall x,y og z slik at:

/div>
hvis n er et sammensatt tall (n = pq), kan en utvidelse for 4 / n bli funnet fra en utvidelse av enten 4 / p eller 4 / q. således, hvis en moteksempel eksisterer, må den minste n som danner en moteksempel være et primtall. Dette resultatet bli ytterligere begrenset til en av seks uendelig aritmetiske progresjoner modulo 840 (Mordell, 1967).

formodningen er oppkalt etter matematikere paul erdaukurs og ernst g. straus som formulerte det i 1948. Det er fortsatt uprøvd fra 2019. Den Diofantiske versjonen av ligningen vises når man multipliserer med nevnen på begge sider og får sin polynomform:

For n=5 for instance, there are two solutions:

Solutions for n = 5 and a) x=2, y=5, z=10 and b) x=2, y=4, z=20 Euler’s Sum of Powers Conjecture
Leonard Euler in 1769 incorrectly conjectured that Diophantine equations of the form

That is,
Euler's sum of powers conjecture
For all integers n and k greater than 1, if the sum of the n kth powers of positive integers is itself a kth power, then n is greater than or equal to k.Det vil si at hvis summen av de første n-betingelsene i enᵏ er lik et begrep som selv er en kth-kraft(f. eks. Formodningen ble motbevist i 1966 Av Lander og Parkin gjennom datasøk, da de oppdaget en moteksempel for saken k = 5, annonsert i det såkalte «korteste papiret som noensinne er publisert»:

Lander & parkin (1966). Moteksempel Til Eulers Formodning om Summer Av Like Krefter. Bulletin Av American Mathematical Society, 72 (6). sider 1079. det spesielle tilfellet av k = 4 ble senere motbevist Av Elkies (1986) som oppdaget en metode for å konstruere uendelige serier av moteksempler. Hans minste moteksempel var: