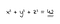
Diophantine ecuaciones han estado en las noticias últimamente. Esto porque, el 6 de septiembre de 2019, un equipo liderado por investigadores de la Universidad de Bristol y el MIT anunció que habían descubierto la solución final al llamado problema de «sumas de tres cubos», que pide soluciones enteras a la ecuación x3 + y3 + z3 = k para valores de k entre 1 y 100. Desde su formulación en 1954 en la Universidad de Cambridge, hasta 2016, se habían encontrado todas las soluciones excepto dos, para k=33 y k=42. En marzo de este año, el matemático Andrew R. Booker en un artículo publicado en arXiv.org anunció que había encontrado la solución correcta para k = 33 usando semanas de tiempo de cómputo en la supercomputadora de Bristol. Su solución, presentada en el artículo «Cracking the problem with 33» es:

Entonces, hace apenas una semana, de nuevo se supo la noticia: k=42 había sido descubierto, de nuevo por Booker junto con otro Andrew, Andrew Sutherland en el MIT, utilizando el llamado Motor de Caridad de fuentes colectivas. Su respuesta es:

Para los valores de k entre 1 y 1000, las soluciones siguen siendo para ser encontrado por los enteros 114, 165, 390, 579, 627, 633, 732, 906, 921 y 975.
El problema de sumas de tres cubos es un ejemplo de un problema que pide soluciones a una ecuación diofántica, que puede definirse como:
Definition
A Diophantine equation is an algebraic equation with several unknowns and integer coefficients.
Es decir, las ecuaciones diofánticas son ecuaciones que presentan varias variables desconocidas (x, y, z,..) cuyas soluciones (=0) sólo aparecen cuando los coeficientes de la ecuación (a, b, c, …) son enteros ( … ,-2, -1, 0, 1, 2, … ).
La Ecuación Diofántica Lineal
Una ecuación diofántica lineal es una ecuación de primer grado cuyas soluciones están restringidas a enteros. El prototipo lineal de la ecuación de Diophantine es:
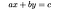
donde a, b y c son enteros y los coeficientes de x y y son variables. Por lo tanto, los problemas diofánticos lineales típicos implican cantidades enteras, como por ejemplo (Brilliant.org, 2019):
How many ways are there to make $2.00 from only nickels and quarters?
Las soluciones al problema se encuentran asignando variables al número de centavos (x) y al número de cuartos (y). Sabemos que $2 es 200 centavos (c), y que un níquel vale 5 centavos (a) y un cuarto de 25 centavos (b). Por lo tanto, llegamos fácilmente a la ecuación especificando el número de formas en que podemos tener $2.00 en centavos y cuartos:

Ahora, porque esta es una sola ecuación con dos incógnitas, no podemos resolver de una variable a la vez (como se podría hacer con un típico sistema de ecuaciones lineales). En su lugar, para el caso lineal, podemos usar el siguiente teorema:
Linear Diophantine equations have integer solutions if and only if c is a multiple of the greatest common divisor of a and b.If integers (x, y) constitute a solution to the linear Diophantine equation for given a, b and c, then the other solutions have the form (x + kv, y - ku) where k is an arbitrary integer and u and v are the quotients of a and b (respectively) by the greatest common divisors of a and b.
El mayor divisor común (GCD) de dos o más enteros, que no son todos cero, es el entero positivo más grande que divide cada uno de los enteros. Para nuestro ejemplo, podemos empezar por dividir fuera de la común divisor 5, la obtención de:

El máximo común divisor de a y b, 1 y 5, es 1. Cualquier c no negativo es un múltiplo de 1. Hay nueve múltiplos de 5 que son menores o iguales a 40. Lo son 0, 5, 10, 15, 20, 25, 30, 35, 40. Por lo tanto, hay nueve maneras de ganar nick 2.00 con monedas de cinco centavos y monedas. Son:
(0, 8), (5, 7), (10, 6), (15, 5), (20, 4), (25, 3), (30, 2), (35, 1) og (40, 0).
El proceso anterior es una versión simple de lo que se llama análisis diofántico, el proceso requerido para encontrar soluciones a ecuaciones diofánticas. Las preguntas que se suelen hacer durante estos análisis son:
- ¿Hay alguna solución?
- ¿Hay soluciones más allá de algunas que se encuentren fácilmente mediante inspección?
- ¿Hay muchas soluciones finitas o infinitas?
- ¿Se pueden encontrar todas las soluciones, en teoría?
- ¿Se puede calcular en la práctica una lista completa de soluciones?
Las técnicas populares utilizadas para resolver ecuaciones diofánticas incluyen descomposición de factores, delimitación por desigualdades, parametrización, aritmética modular, inducción, descenso infinito de Fermat, reducción a Pell y fracciones continuas, sistemas numéricos posicionales y curvas elípticas (Wikiversidad, 2019).
La ecuación de Hardy-Ramanujan
El número de Hardy-Ramanujan 1729, conocido como «número de taxi», se define como «el número más pequeño expresable como la suma de dos cubos de dos maneras diferentes», a partir de una anécdota del matemático británico G. H. Hardy cuando visitó al matemático indio Srinivasa Ramanujan en el hospital:
» Recuerdo que una vez fui a verlo cuando estaba enfermo en Putney. Viajé en el taxi número 1729 y comenté que el número me parecía bastante aburrido, y que esperaba que no fuera un presagio desfavorable. «No», respondió Ramanujan, » es un número muy interesante; es el número más pequeño que se puede expresar como la suma de dos cubos de dos maneras diferentes.»- G. H. Hardy (1918)
La ecuación en el corazón de los números de taxis es diofantina, es decir, la ecuación:

Las dos formas diferentes 1729 es expresable como la suma de dos cubos son 13 + 123 y 93 + 103. Hasta ahora, se conocen seis números de taxis. Son:
Ta(1) = 2
= 1³ + 1³Ta(2) = 1,729
= 1³ + 12³ = 9³ + 10³Ta(3) = 87,539,319
= 167³ + 436³ = 228³ + 423³ = 255³ + 414³Ta(4) = 6,963,472,309,248
= 2421³ + 19083³ = 5436³ + 18948³ = 10200³ + 18072³ = 13322³ + 16630³Ta(5) = 48,988,659,276,962,496
= 38787³ + 365757³ = 107839³ + 362753³ = 205292³ + 342952³ = 221424³ + 336588³ =231518³ + 331954³Ta(6) = 24,153,319,581,254,312,065,344
= 582162³ + 28906206³ = 3064173³ + 28894803³ = 8519281³ + 28657487³ = 16218068³ + 27093208³ = 17492496³ + 26590452³ = 18289922³ + 26224366³
Último teorema de Fermat

Los números expresables como la suma de cubos (como los del problema de la suma de tres cubos y el número de Hardy-Ramanujan) fueron mencionados por primera vez en 1657 por Bernard Frénicle de Bessy, propiedad citando el ejemplo del número 1729 en sus correspondencias con John Wallis y Pierre de Fermat. Desde entonces, el nombre de Fermat se ha convertido en sinónimo del caso más general del problema, siguiendo su afirmación de 1637 en el margen de una copia de Arithmetica de Diophantus de que no hay tres enteros positivos a, b y c que satisfagan la ecuación diofántica
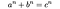
Que Fermat (en)declaró que había demostrado ser cierto para valores enteros de n mayores que 2, pero que no pudo incluir en sus notas en el libro porque el margen era demasiado estrecho:
Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet - Pierre de Fermat, 1637
Traducido, su texto dice: «Es imposible que un cubo sea la suma de dos cubos, que una cuarta potencia sea la suma de dos cuartas potencias, o en general que cualquier número que sea una potencia mayor que la segunda sea la suma de dos potencias similares. He descubierto una demostración verdaderamente maravillosa de esta proposición de que este margen es demasiado estrecho para contenerlo.»(Nagell, 1951).
La conjetura fue finalmente probada después de 358 años en 1994 por el matemático inglés Andrew Wiles en su artículo Modular elliptic curves y el último Teorema de Fermat publicado en the Annals of Mathematics 141 (3), pp 443-551. La prueba por contradicción de Wiles, de 129 páginas, utiliza técnicas de geometría algebraica y teoría de números para probar un caso especial del teorema de modularidad para curvas elípticas, que junto con el teorema de Ribet implica la verdad del último teorema de Fermat. Debido a su extenso uso de las matemáticas modernas, es cierto que la prueba de Wiles no puede ser la misma que Fermat afirma haber encontrado, que todavía permanece perdida (y probablemente no fue una prueba en absoluto).
Triples pitagóricos
La ecuación diofántica quizás más conocida de todas es un caso particular de la ecuación del Último Teorema de Fermat, pero para n = 2. Esta es la ecuación que nos ayuda a encontrar la longitud de los lados de un ángulo recto del triángulo
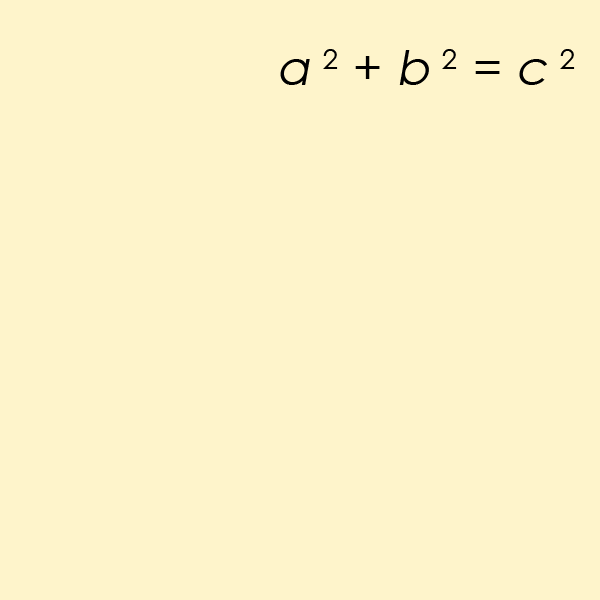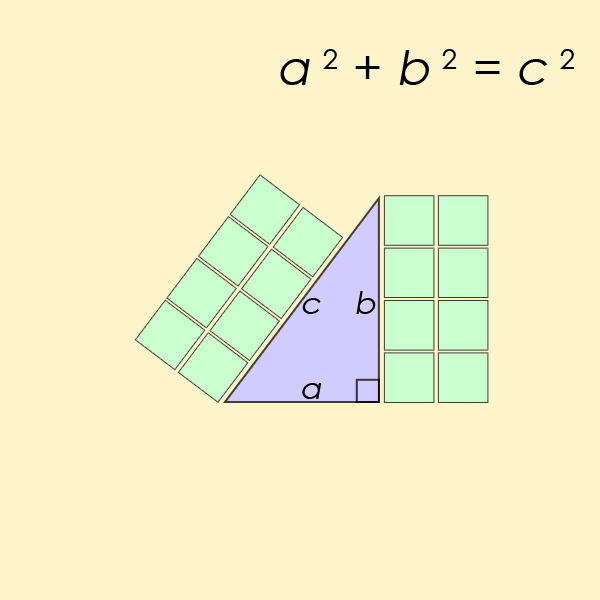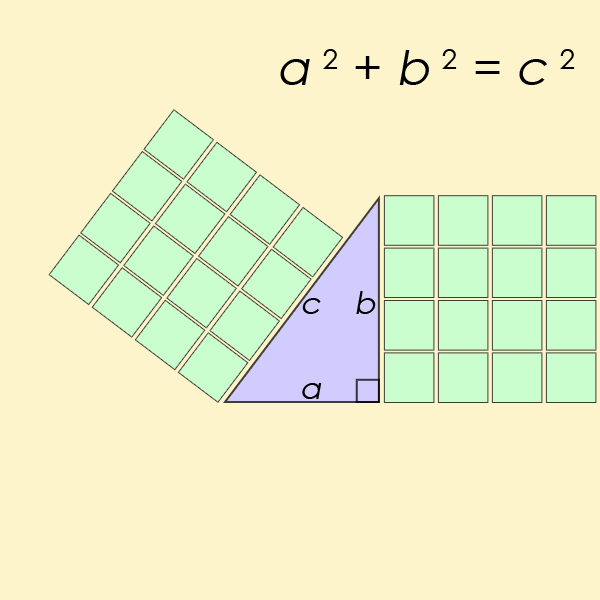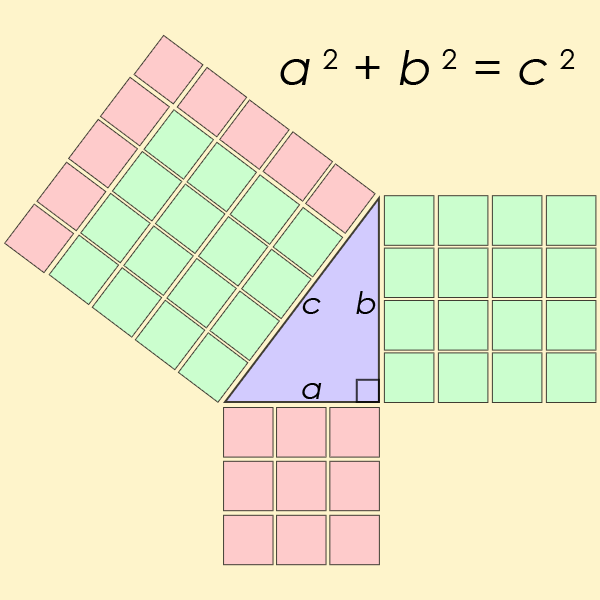
Ecuación de Pell
La ecuación de Pell (a veces la ecuación de Pell-Fermat) es cualquier ecuación de la siguiente forma donde n es un entero positivo sin cuadrados dado y se buscan soluciones enteras para x e y:

Esta ecuación Diophantine primero fue estudiado ampliamente por el matemático Indio Brahmagupta todo el año 628. Desarrolló el llamado método chakravala para resolverlo y otras ecuaciones indeterminadas. Esto unos mil años antes de su homónimo, el matemático inglés John Pell (1611-1685) lo estudió mientras trabajaba con Johann Heinrich Rahn. Su nombre surgió de una atribución errónea de una solución proporcionada por Lord Brouncker a Pell por Leonard Euler en 1732-33.
Se sabe que las ecuaciones de la forma de la ecuación de Pell con n = 2 se estudiaron ya en el año 400 a. C. tanto en India como en Grecia, además del caso en el que x2 − 2y2 = -1, debido a la conexión de estas dos ecuaciones con el número irracional obtenido del cálculo de la raíz cuadrada de 2 (si x e y son enteros positivos que satisfacen esta ecuación, entonces x/y es una aproximación de √2).
En coordenadas cartesianas, la ecuación tiene la forma de una hipérbola, ya que las soluciones a la ecuación ocurren donde la curva pasa a través de un punto cuyas coordenadas x e y son ambos enteros, como x = 1, y = 0 y x = -1, y = 0. Lagrange demostró que mientras n no sea un cuadrado perfecto, la ecuación de Pell tiene infinitas soluciones enteras distintas.
La Conjetura de Erdős-Straus
La conjetura de Erdős–Straus establece que para cada entero mayor que 2, el número racional 4 / n puede expresarse como la suma de tres fracciones unitarias positivas. Es decir, para cada entero n ≥ 2, existen enteros positivos x,y y z tales que:

Si n es un número compuesto (n = pq), entonces se puede encontrar una expansión para 4/n a partir de una expansión de 4/p o 4/q. Por lo tanto, si existe un contraejemplo, el n más pequeño que forma un contraejemplo tendría que ser un número primo. Este resultado se restringirá a una de las seis progresiones aritméticas infinitas módulo 840 (Mordell, 1967).

La conjetura es nombrado después de que los matemáticos Paul Erdős y Ernst G. Straus que formulado en 1948. Sigue sin probarse a partir de 2019. La versión diofántica de la ecuación aparece cuando se multiplica por el denominador en ambos lados y se obtiene su forma polinómica:

For n=5 for instance, there are two solutions:

Euler’s Sum of Powers Conjecture
Leonard Euler in 1769 incorrectly conjectured that Diophantine equations of the form

That is,
Euler's sum of powers conjecture
For all integers n and k greater than 1, if the sum of the n kth powers of positive integers is itself a kth power, then n is greater than or equal to k.
Es decir, que si la suma de los primeros n términos de a is es igual a un término que es en sí mismo una potencia k (por ejemplo, b b), entonces n debe ser mayor o igual a k. La conjetura fue un intento de Euler de generalizar el último teorema de Fermat. La conjetura fue refutada en 1966 por Lander y Parkin a través de una búsqueda por computadora, cuando descubrieron un contraejemplo para el caso k=5, anunciado en el llamado «artículo más corto jamás publicado»:

El caso especial de k = 4 fue posteriormente desmentido por Elkies (1986), quien descubrió un método para construir series infinitas de contraejemplos. Su contraejemplo más pequeño fue: