wtedy, zaledwie tydzień temu, znowu rozeszła się wiadomość: K=42 został ponownie odkryty przez Bookera wraz z innym Andrew, Andrew Sutherlandem z mit, za pomocą tak zwanego silnika charytatywnego. Ich odpowiedź brzmi::

dla wartości k z zakresu od 1 do 1000, nadal można znaleźć rozwiązania dla liczb całkowitych 114, 165, 390, 579, 627, 633, 732, 906, 921 i 975.

problem Sum trzech kostek jest przykładem problemu wymagającego rozwiązania równania Diofantyny, które można zdefiniować jako:

Definition
A Diophantine equation is an algebraic equation with several unknowns and integer coefficients.

czyli równania Diofantyny są równaniami zawierającymi kilka nieznanych zmiennych (x, y,Z,..), których rozwiązania (=0) pojawiają się tylko wtedy, gdy współczynniki równania (A, b, c,…) są liczbami całkowitymi ( … ,-2, -1, 0, 1, 2, … ).

liniowe równanie Diofantyny

liniowe równanie Diofantyny jest równaniem pierwszego stopnia, którego rozwiązania są ograniczone do liczb całkowitych. Prototypowe liniowe równanie Diofantyny to:

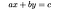
gdzie A, B I C są współczynnikami całkowitymi, a X i y są zmiennymi. Typowe liniowe problemy Diofantynowe wiążą się więc z całymi ilościami, takimi jak np. (Brilliant.org, 2019):

How many ways are there to make $2.00 from only nickels and quarters?

rozwiązanie problemu można znaleźć poprzez przypisanie zmiennych do liczby nickeli (x) i liczby ćwiartek (y). Wiemy, że 2 dolary to 200 centów (c), a grosz jest wart 5 centów (a) i ćwierć 25 centów (b). W ten sposób łatwo dojdziemy do równania określającego liczbę sposobów, w których możemy mieć $2.00 w niklach i ćwiartkach:

teraz, ponieważ jest to jedno równanie z dwoma niewiadomymi, nie możemy rozwiązać dla jednej zmiennej naraz (jak można to zrobić z typowym układem równań liniowych). Zamiast tego, dla przypadku liniowego, możemy użyć następującego twierdzenia:

Linear Diophantine equations have integer solutions if and only if c is a multiple of the greatest common divisor of a and b.If integers (x, y) constitute a solution to the linear Diophantine equation for given a, b and c, then the other solutions have the form (x + kv, y - ku) where k is an arbitrary integer and u and v are the quotients of a and b (respectively) by the greatest common divisors of a and b.

największy wspólny dzielnik (GCD) dwóch lub więcej liczb całkowitych, które nie są wszystkie zer, jest największą dodatnią liczbą całkowitą, która dzieli każdą z liczb całkowitych. W powyższym przykładzie możemy zacząć od obliczenia wspólnego dzielnika 5, uzyskując:

największym wspólnym dzielnikiem a i B, 1 i 5, jest 1. Każde nie-ujemne c jest wielokrotnością 1. Istnieje dziewięć takich wielokrotności 5, które są mniejsze lub równe 40. Są to 0, 5, 10, 15, 20, 25, 30, 35, 40. Dlatego istnieje dziewięć sposobów na zarobienie $2.00 z pięciocentówek i ćwierćdolarówek. Są to:

(0, 8), (5, 7), (10, 6), (15, 5), (20, 4), (25, 3), (30, 2), (35, 1) og (40, 0)

powyższy proces jest prostą wersją tzw. analizy Diofantynowej, procesu wymaganego do znalezienia rozwiązań równań Diofantynowych. Najczęściej zadawane podczas takich analiz pytania to:

• czy są jakieś rozwiązania?
• czy są jakieś rozwiązania poza niektórymi, które łatwo znaleźć poprzez inspekcję?
• czy istnieje nieskończenie wiele rozwiązań?
• czy w teorii można znaleźć wszystkie rozwiązania?
• czy można w praktyce obliczyć pełną listę rozwiązań?

popularne techniki używane do rozwiązywania równań Diofantynowych obejmują rozkład czynnika, ograniczanie przez nierówności, parametryzację, arytmetykę modularną, indukcję, nieskończone zejście Fermata, redukcję do ułamków Pella i ciągłych, pozycyjne systemy liczbowe i krzywe eliptyczne (Wikiversity, 2019).

równanie Hardy 'ego-Ramanujana

Liczba Hardy’ ego-Ramanujana 1729, znana jako „numer taksówki” jest zdefiniowana jako „najmniejsza liczba wyrażalna jako suma dwóch sześcianów na dwa różne sposoby”, z anegdoty brytyjskiego matematyka G. H. Hardy kiedy on odwiedzać indyjski matematyk Srinivasa Ramanujan w the Szpital:

” i pamiętam raz iść zobaczyć go gdy on być chory w Putney. Jechałem taksówką numer 1729 i zauważyłem, że numer wydawał mi się raczej nudny i miałem nadzieję, że nie był to niekorzystny omen. „Nie,” odpowiedział Ramanujan, ” jest to bardzo interesująca liczba; jest to najmniejsza liczba wyrażalna jako suma dwóch sześcianów na dwa różne sposoby.”- G. H. Hardy (1918)

równaniem w sercu liczb taksonomicznych jest Diofantyna, czyli równanie:

dwa różne sposoby 1729 można wyrazić, ponieważ suma dwóch sześcianów wynosi 13 + 123 i 93 + 103. Do tej pory znanych jest sześć numerów taksówek. Są to:

Ta(1) = 2 
= 1³ + 1³Ta(2) = 1,729 
= 1³ + 12³ = 9³ + 10³Ta(3) = 87,539,319 
= 167³ + 436³ = 228³ + 423³ = 255³ + 414³Ta(4) = 6,963,472,309,248 
= 2421³ + 19083³ = 5436³ + 18948³ = 10200³ + 18072³ = 13322³ + 16630³Ta(5) = 48,988,659,276,962,496
= 38787³ + 365757³ = 107839³ + 362753³ = 205292³ + 342952³ = 221424³ + 336588³ =231518³ + 331954³Ta(6) = 24,153,319,581,254,312,065,344
= 582162³ + 28906206³ = 3064173³ + 28894803³ = 8519281³ + 28657487³ = 16218068³ + 27093208³ = 17492496³ + 26590452³ = 18289922³ + 26224366³

Ostatnie twierdzenie Fermata

liczby wyrażone jako suma kostek (takie jak te z problemu sumy trzech kostek i liczby Hardy ’ ego-ramanujana) zostały po raz pierwszy wspomniane w 1657 roku przez Bernarda frénicle de Bessy, który opisał własność przytaczając przykład liczby 1729 w korespondencji z Johnem wallisem i Pierre de Fermat. Nazwa fermata od tego czasu stała się nieco synonimem bardziej ogólnego przypadku problemu, po jego 1637 twierdzeniu na marginesie kopii arytmetyki Diophantus, że żadne trzy dodatnie liczby całkowite A, b I c nie spełniają równania Diofantyny

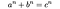
które FERMAT (in)stwierdził, że okazały się prawdziwe dla wartości całkowitych N większych niż 2, ale których nie mógł zawrzeć w swoich notatkach w książce, ponieważ margines był zbyt wąski:

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet - Pierre de Fermat, 1637

przetłumaczony tekst brzmi „niemożliwe jest, aby sześcian był sumą dwóch sześcianów, czwarta potęga była sumą dwóch czwartych potęg, lub ogólnie dla dowolnej liczby, która jest potęgą większą niż druga, aby była sumą dwóch podobnych potęg. Odkryłem naprawdę cudowną demonstrację tej propozycji, że ten margines jest zbyt wąski, aby go zawrzeć.”(Nagell, 1951).

przypuszczenie zostało ostatecznie udowodnione po 358 latach w 1994 roku przez angielskiego matematyka Andrew Wilesa w jego pracy Modular elliptic curves and Fermat ’ S Last Theorem opublikowanej w The Annals of Mathematics 141 (3), s. 443-551. Wiles ’ proof by contradiction, liczący 129 stron, wykorzystuje techniki geometrii algebraicznej i teorii liczb do udowodnienia szczególnego przypadku twierdzenia modularności dla krzywych eliptycznych, które wraz z twierdzeniem Ribeta implikuje prawdę ostatniego twierdzenia Fermata. Ze względu na szerokie zastosowanie nowoczesnej matematyki, jest pewne, że dowód Wilesa nie może być tym samym, o którym twierdzi Fermat — który nadal pozostaje zaginiony (i prawdopodobnie nie był wcale dowodem).

Trójki pitagorejskie

być może najbardziej znanym równaniem Diofantynowym ze wszystkich jest szczególny przypadek równania z ostatniego twierdzenia Fermata, ale dla n=2. Jest to równanie, które pomaga znaleźć długość boków trójkąta prostokątnego

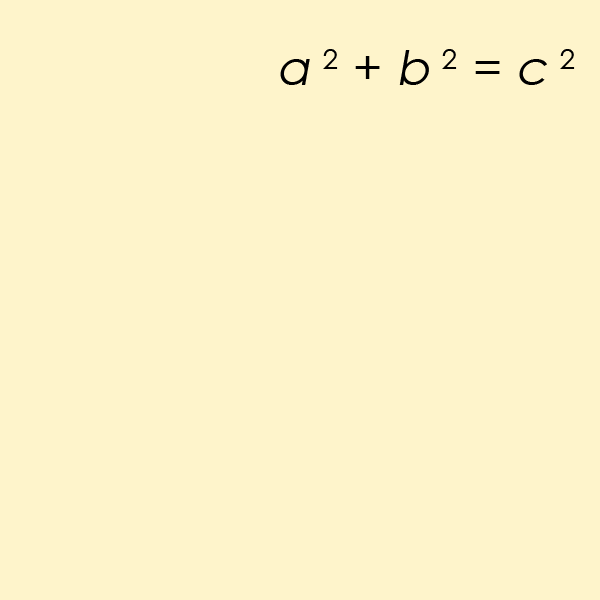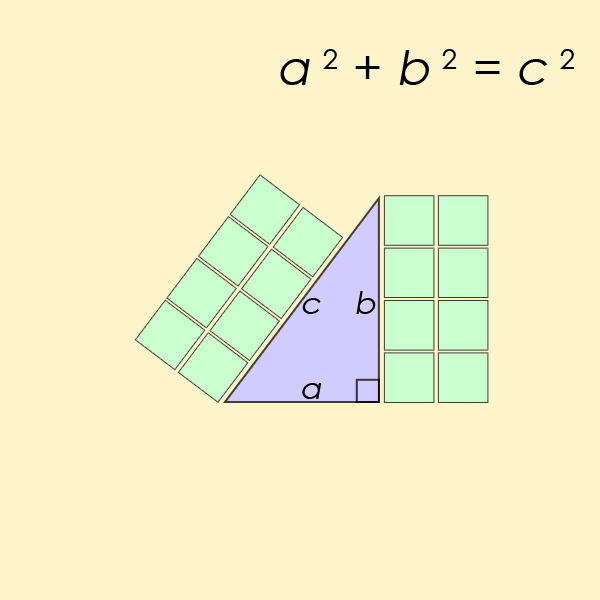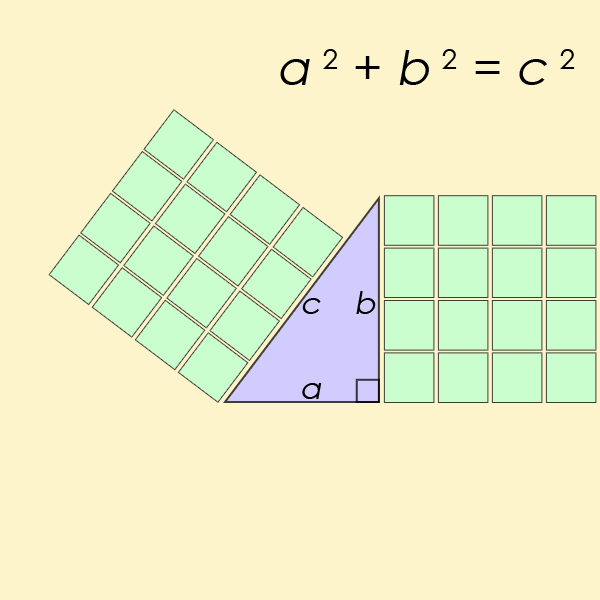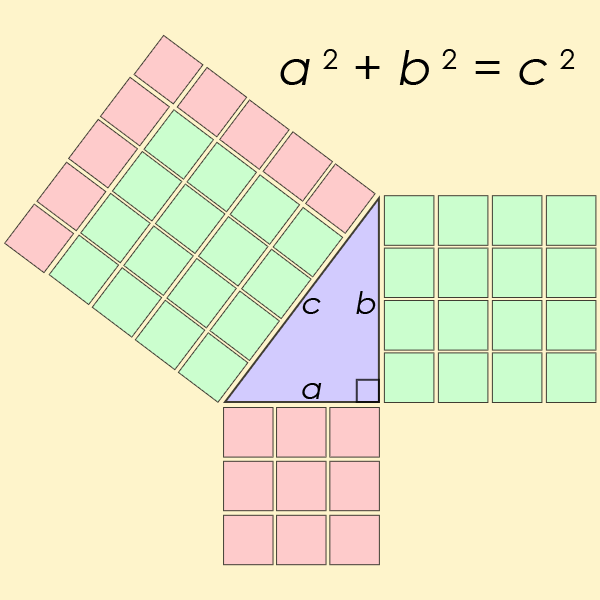
równanie Pella

równanie Pella (czasami równanie Pella-Fermata) jest dowolnym równaniem o następującej postaci, w której n jest daną dodatnią liczbą całkowitą bez kwadratu, a rozwiązania całkowite są poszukiwane dla x i y:

to równanie diofantyny zostało po raz pierwszy szeroko zbadane przez indyjskiego matematyka brahmaguptę około roku 628. Opracował tzw. metodę chakrawali do jej rozwiązywania oraz inne równania nieokreślone. To około tysiąca lat przed jego imiennikiem, angielski matematyk John Pell (1611-1685) badał go podczas pracy pod kierunkiem Johanna Heinricha rahna. Jego nazwa powstała z błędnego przypisania Pellowi rozwiązania zaproponowanego przez Lorda Brounckera przez Leonarda Eulera w latach 1732-33.

równania postaci równania Pella z n = 2 są znane jako badane już w 400 pne w Indiach i Grecji, oprócz przypadku, gdy x2 − 2Y2 = -1, z powodu połączenia tych dwóch równań z irracjonalną liczbą uzyskaną z obliczenia pierwiastka kwadratowego z 2 (Jeśli x i y są dodatnimi liczbami całkowitymi spełniającymi to równanie, to x/y jest przybliżeniem √2).

we współrzędnych kartezjańskich równanie ma postać hiperboli, ponieważ rozwiązania równania występują wszędzie tam, gdzie krzywa przechodzi przez punkt, którego współrzędne X i Y są liczbami całkowitymi, takimi jak x = 1, y = 0 i x = -1, y = 0. Lagrange udowodnił, że dopóki n nie jest kwadratem doskonałym, równanie Pella ma nieskończenie wiele różnych rozwiązań całkowitych.

domysł Erdősa–Strausa

domysł Erdősa–Strausa mówi, że dla każdej liczby całkowitej większej od 2, wymierna liczba 4 / N może być wyrażona jako suma trzech dodatnich ułamków jednostkowych. Oznacza to, że dla każdej liczby całkowitej N ≥ 2 istnieją dodatnie liczby całkowite x, y i z takie,że:

Jeśli N jest liczbą złożoną (N = PQ), to rozszerzenie dla 4/N można znaleźć z rozszerzenia o 4/P lub 4 / q. tak więc, jeśli istnieje kontrprzykład, najmniejsze N tworzące kontrprzykład musiałoby być liczbą pierwszą. Wynik ten można dodatkowo ograniczyć do jednej z sześciu nieskończonych progresji arytmetycznych modulo 840 (Mordell, 1967).

przypuszczenie zostało nazwane na cześć matematyków Paula Erdősa i Ernsta G. Strausa, którzy sformułowali je w 1948 roku. Od 2019 pozostaje niesprawdzony. Diofantyczna wersja równania pojawia się, gdy mnożymy przez mianownik po obu stronach i otrzymujemy jego postać wielomianową:

For n=5 for instance, there are two solutions:

Euler’s Sum of Powers Conjecture

Leonard Euler in 1769 incorrectly conjectured that Diophantine equations of the form

That is,

Euler's sum of powers conjecture
For all integers n and k greater than 1, if the sum of the n kth powers of positive integers is itself a kth power, then n is greater than or equal to k.

oznacza to, że jeśli suma pierwszych n wyrazów aᵏ jest równa wyrażeniu, które samo w sobie jest potęgą kth (np. bᵏ), to n musi być większe lub równe K. przypuszczenie było próbą uogólnienia ostatniego twierdzenia Fermata przez Eulera. Hipoteza ta została obalona w 1966 roku przez Landera i Parkina za pomocą wyszukiwania komputerowego, kiedy odkryli kontrprzykład dla przypadku k = 5, ogłoszony w tak zwanym „najkrótszym dokumencie kiedykolwiek opublikowanym”:

szczególny przypadek k = 4 został później obalony przez Elkiesa (1986), który odkrył metodę konstruowania nieskończonych serii kontrprzykładów. Jego najmniejszym kontrprzykładem było: