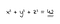
diofantine ekvationer har varit i nyheterna nyligen. Detta för att den 6 September 2019 meddelade ett team som leds av forskare vid University of Bristol och MIT att de hade upptäckt den slutliga lösningen på det så kallade ”summan av tre kuber”-problemet, som ber om heltalslösningar på ekvationen x3 + y3 + z3 = k för värden på k mellan 1 och 100. Sedan dess formulering 1954 vid University of Cambridge, fram till 2016, hade varje lösning hittats utom två, för k=33 och k=42. I Mars i år, matematiker Andrew R. Booker i ett papper publicerat på arXiv.org meddelade att han hade hittat den rätta lösningen för k=33 Med hjälp av veckors beräkningstid på Bristols superdator. Hans lösning, som presenteras i papperet ”knäcka problemet med 33” är:

sedan, för bara en vecka sedan, bröt nyheten igen: k=42 hade upptäckts, igen av Booker tillsammans med en annan Andrew, Andrew Sutherland på mit, med hjälp av den folkmassade så kallade välgörenhetsmotorn. Deras svar är:

för värden på K mellan 1 och 1000 finns det fortfarande lösningar för heltalen 114, 165, 390, 579, 627, 633, 732, 906, 921 och 975.
summan av tre kuber problem är ett exempel på ett problem som ber om lösningar på en Diofantin ekvation, som kan definieras som:
Definition
A Diophantine equation is an algebraic equation with several unknowns and integer coefficients.
det vill säga,Diofantin ekvationer är ekvationer med flera okända variabler (x, y, z,..) vars lösningar (=0) endast visas när ekvationens koefficienter (a, b, c, …) är heltal ( … ,-2, -1, 0, 1, 2, … ).
den linjära Diofantin ekvationen
en linjär Diofantin ekvation är en ekvation av den första graden vars lösningar är begränsade till heltal. Den prototypiska linjära diofantin ekvationen är:
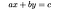
där A, B och C är heltalskoefficienter och X och Y är variabler. Typiska linjära Diofantinproblem involverar därför hela mängder, såsom t.ex. (Brilliant.org, 2019):
How many ways are there to make $2.00 from only nickels and quarters?
lösningarna på problemet hittas genom att tilldela variabler till antalet nickels (x) och antalet kvartal (y). Vi vet att $2 är 200 cent (c), och att en nickel är värt 5 cent (a) och en fjärdedel 25 cent (b). Således kommer vi lätt fram till ekvationen som anger antalet sätt på vilka vi kan ha $2,00 i nickels och kvartaler:

nu, eftersom det här är en enda ekvation med två okända, kan vi inte lösa för en variabel i taget (som man kan göra med ett typiskt system av linjära ekvationer). Istället för det linjära fallet kan vi använda följande sats:
Linear Diophantine equations have integer solutions if and only if c is a multiple of the greatest common divisor of a and b.If integers (x, y) constitute a solution to the linear Diophantine equation for given a, b and c, then the other solutions have the form (x + kv, y - ku) where k is an arbitrary integer and u and v are the quotients of a and b (respectively) by the greatest common divisors of a and b.
den största gemensamma delaren (GCD) av två eller flera heltal, som inte alla är noll, är det största positiva heltalet som delar var och en av heltalen. För vårt exempel ovan kan vi börja med att factoring ut den gemensamma delaren 5, erhålla:

den största gemensamma delaren av A och B, 1 och 5, är 1. Alla icke-negativa c är en multipel av 1. Det finns nio sådana multiplar av 5 som är mindre än eller lika med 40. De är 0, 5, 10, 15, 20, 25, 30, 35, 40. Därför finns det nio sätt att göra $2,00 från nickels och kvartaler. De är:
(0, 8), (5, 7), (10, 6), (15, 5), (20, 4), (25, 3), (30, 2), (35, 1) och (40, 0).
ovanstående process är en enkel version av vad som kallas Diofantinanalys, den process som krävs för att hitta lösningar på Diofantin ekvationer. De frågor som vanligtvis ställs under sådana analyser är:
- finns det några lösningar?
- finns det några lösningar utöver några som lätt kan hittas genom inspektion?
- finns det ändligt eller oändligt många lösningar?
- kan alla lösningar hittas, i teorin?
- kan man i praktiken beräkna en fullständig lista över lösningar?
populära tekniker som används för att lösa Diofantinekvationer inkluderar faktornedbrytning, begränsning av ojämlikhet, parametrisering, modulär aritmetik, induktion, Fermats oändliga nedstigning, reduktion till Pells och fortsatta fraktioner, positionella talsystem och elliptiska kurvor (Wikiversity, 2019).
Hardy-Ramanujan ekvationen
Hardy-Ramanujan nummer 1729, känd som en ”taxi cab nummer” definieras som ”det minsta antalet uttrycks som summan av två kuber på två olika sätt”, från en anekdot av den brittiska matematikern G. H. Hardy när han besökte Indisk matematiker Srinivasa Ramanujan på sjukhuset:
” Jag kommer ihåg att jag en gång skulle träffa honom när han var sjuk i Putney. Jag hade ridit i taxi nummer 1729 och påpekade att numret tycktes mig ganska tråkigt, och att jag hoppades att det inte var ett ogynnsamt omen. ”Nej,” svarade Ramanujan, ” det är ett mycket intressant tal; det är det minsta tal som uttrycks som summan av två kuber på två olika sätt.”- G. H. Hardy (1918)
ekvationen i hjärtat av taxikabnummer är Diofantin, nämligen ekvationen:

de två olika sätten 1729 kan uttryckas eftersom summan av två kuber är 13 + 123 och 93 + 103. Hittills är sex taxibilar kända. De är:
Ta(1) = 2
= 1³ + 1³Ta(2) = 1,729
= 1³ + 12³ = 9³ + 10³Ta(3) = 87,539,319
= 167³ + 436³ = 228³ + 423³ = 255³ + 414³Ta(4) = 6,963,472,309,248
= 2421³ + 19083³ = 5436³ + 18948³ = 10200³ + 18072³ = 13322³ + 16630³Ta(5) = 48,988,659,276,962,496
= 38787³ + 365757³ = 107839³ + 362753³ = 205292³ + 342952³ = 221424³ + 336588³ =231518³ + 331954³Ta(6) = 24,153,319,581,254,312,065,344
= 582162³ + 28906206³ = 3064173³ + 28894803³ = 8519281³ + 28657487³ = 16218068³ + 27093208³ = 17492496³ + 26590452³ = 18289922³ + 26224366³
Fermats sista sats

tal som uttrycks som summan av kuber (som de från summan av tre kubproblem och Hardy-Ramanujan-numret) nämndes först 1657 av Bernard fr fastigheten citerar exemplet med numret 1729 i hans korrespondenser med John Wallis och Pierre de Fermat. Fermats namn har sedan dess blivit något synonymt med det mer allmänna fallet av problemet, efter hans 1637 påstående i marginalen av en kopia av Diophantus’ Arithmetica att inga tre positiva heltal a, b och c uppfyller Diofantin ekvationen
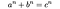
som Fermat (in)berömt uppgav att han hade visat sig vara sant för heltalsvärden på N större än 2, men som han inte kunde inkludera i sina anteckningar i boken eftersom marginalen var för smal:
Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet - Pierre de Fermat, 1637
översatt, hans text läser ” det är omöjligt för en kub att vara summan av två kuber, en fjärde kraft att vara summan av två fjärde krafter, eller i allmänhet för ett tal som är en kraft större än den andra för att vara summan av två liknande krafter. Jag har upptäckt en verkligt fantastisk demonstration av detta förslag att denna marginal är för smal för att innehålla.”(Nagell, 1951).
gissningen bevisades slutligen efter 358 år 1994 av den engelska matematikern Andrew Wiles i hans papper Modular elliptic curves och Fermats sista sats publicerad i Annals of Mathematics 141 (3), s 443-551. Wiles bevis genom motsägelse, på 129 sidor lång, använder tekniker från algebraisk geometri och talteori för att bevisa ett speciellt fall av modularitetssatsen för elliptiska kurvor, som tillsammans med Ribets sats antyder sanningen i Fermats sista sats. På grund av sin omfattande användning av modern matematik är det säkert att Wiles bevis inte kan vara detsamma som påstås hittas av Fermat — vilket fortfarande är förlorat (och sannolikt inte var ett bevis alls).
Pythagorean tripplar
den kanske mest kända Diofantin ekvationen av alla är ett särskilt fall av ekvationen från Fermats sista sats, men för n=2. Detta är ekvationen som hjälper en att hitta längden på sidorna av en rätvinklig triangel
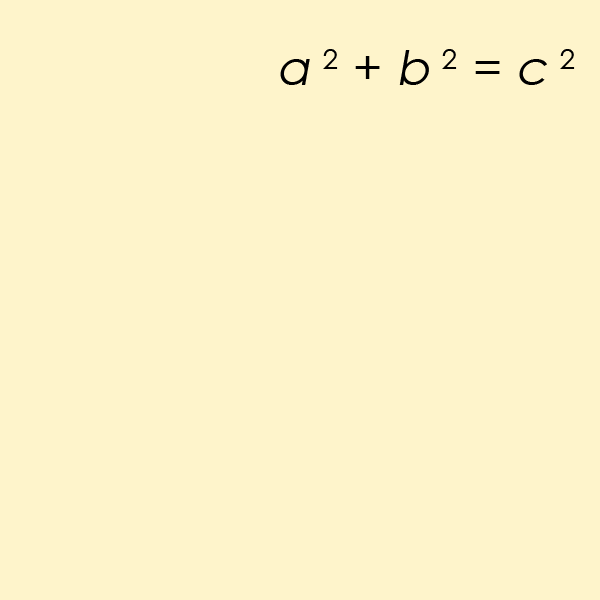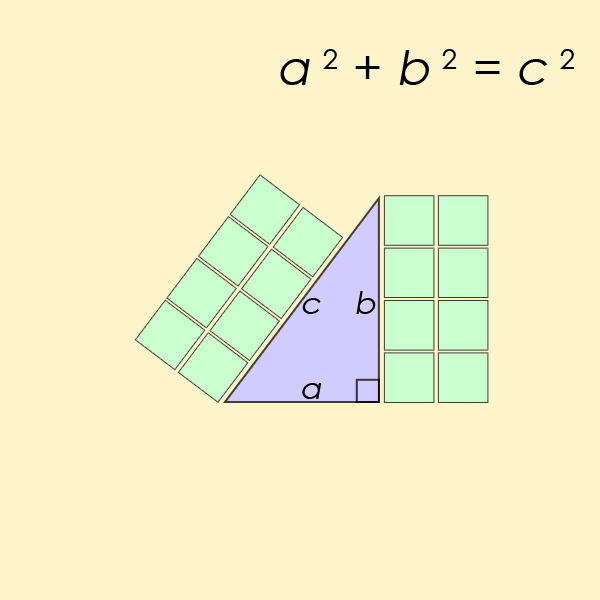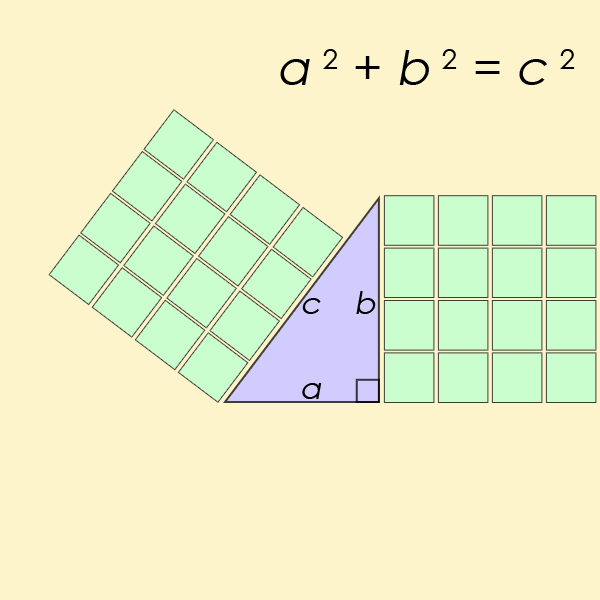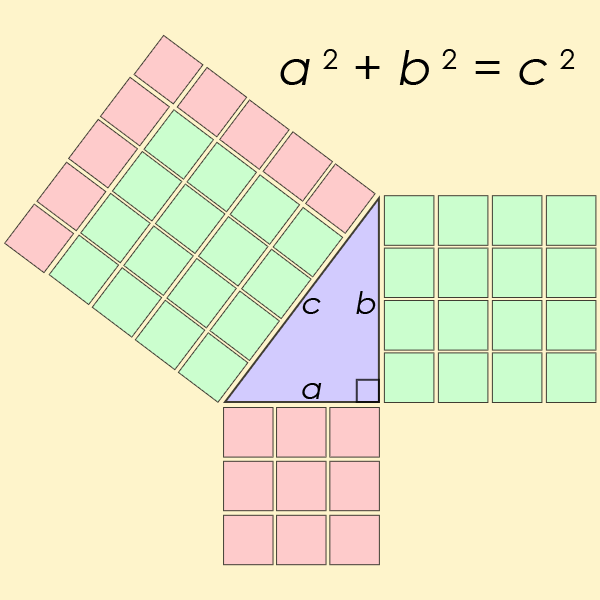
Pells ekvation
Pells ekvation (ibland Pell-Fermat-ekvationen) är någon ekvation av följande form där n är ett givet positivt kvadratfritt heltal och heltalslösningar söks för x och y:

denna diofantiska ekvation studerades först i stor utsträckning av den indiska matematikern Brahmagupta omkring år 628. Han utvecklade den så kallade chakravala-metoden för att lösa den och andra obestämda ekvationer. Detta ungefär tusen år före namnet studerade den engelska matematikern John Pell (1611-1685) den medan han arbetade under Johann Heinrich Rahn. Dess namn uppstod från en felaktig tillskrivning av en lösning från Lord Brouncker till Pell av Leonard Euler 1732-33.
ekvationer av formen av Pells ekvation med n = 2 är kända för att ha studerats så tidigt som 400 f.Kr. i både Indien och Grekland, förutom fallet där x2 − 2y2 = -1, på grund av anslutningen av dessa två ekvationer till det irrationella talet som erhållits vid beräkning av kvadratroten av 2 (om x och y är positiva heltal som uppfyller denna ekvation, är x/y en approximation av 2-talet).
i kartesiska koordinater har ekvationen formen av en hyperbola, eftersom lösningar på ekvationen uppstår varhelst kurvan passerar genom en punkt vars X-och y-koordinater är båda heltal, såsom x = 1, y = 0 och x = -1, y = 0. Lagrange visade att så länge n inte är en perfekt kvadrat, har Pells ekvation oändligt många distinkta heltalslösningar.
erd: s antagande av Ax–Straus
erd: s antagande av Ax–Straus anger att för varje heltal som är större än 2 kan det rationella talet 4/n uttryckas som summan av tre positiva enhetsfraktioner. Det vill säga för varje heltal n 2 finns det positiva heltal X, y och z så att:

om n är ett sammansatt tal (n = PQ), kunde en expansion för 4/n hittas från en expansion av antingen 4/p eller 4 / Q. således,om ett motexempel existerar, måste det minsta n som bildar ett motexempel vara ett primtal. Detta resultat begränsas ytterligare till en av sex oändliga aritmetiska progressioner modulo 840 (Mordell, 1967).

förmodan är uppkallad efter matematiker Paul erd avsugningar och Ernst G. Straus som formulerade det i 1948. Det är fortfarande obevisat från och med 2019. Den diofantinska versionen av ekvationen visas när man multiplicerar med nämnaren på båda sidor och får sin polynomform:

For n=5 for instance, there are two solutions:

Euler’s Sum of Powers Conjecture
Leonard Euler in 1769 incorrectly conjectured that Diophantine equations of the form

That is,
Euler's sum of powers conjecture
For all integers n and k greater than 1, if the sum of the n kth powers of positive integers is itself a kth power, then n is greater than or equal to k.
det vill säga att om summan av de första n-termerna i en Macau är lika med en term som i sig är en kth-kraft (t. ex. Gissningen motbevisades 1966 av Lander och Parkin genom datorsökning, när de upptäckte ett motexempel för fallet k=5, meddelat i det så kallade ”Kortaste papperet som någonsin publicerats”:

det speciella fallet med k = 4 motbevisades senare av Elkies (1986) som upptäckte en metod för att konstruera oändliga serier av motexempel. Hans minsta motexempel var: