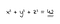
Diophantine equações têm sido notícia recentemente. Isso porque, no dia 6 de setembro de 2019, uma equipe liderada por pesquisadores da Universidade de Bristol e o MIT anunciou que tinha descoberto a solução final para o chamado “soma de três cubos” problema, que pede para o número inteiro soluções para a equação x3 + y3 + z3 = k para valores de k entre 1 e 100. Desde a sua formulação em 1954 na Universidade de Cambridge, até 2016, Todas as soluções foram encontradas exceto duas, para k=33 E k=42. Em março deste ano, o matemático Andrew R. Booker em um artigo publicado sobre arXiv.org anunciou que tinha encontrado a solução correta para K=33 usando semanas de tempo de computação no supercomputador de Bristol. A sua solução, apresentado em papel “Decifrando o problema com 33” é:

Então, apenas uma semana atrás, novamente a notícia: k=42 havia sido descoberto, novamente por Booker, junto com o outro André, André Sutherland no MIT, usando o crowd-sourced chamado Caridade Motor. A resposta deles é::

Para os valores de k entre 1 e 1000, soluções de ainda ser encontrado para a números inteiros 114, 165, 390, 579, 627, 633, 732, 906, 921 e 975.

A soma de três cubos problema é um exemplo de um problema pedindo soluções para uma equação de Diophantine, que pode ser definido como:

Definition
A Diophantine equation is an algebraic equation with several unknowns and integer coefficients.

isto é, Diophantine equações são equações com várias incógnitas (x,y, z, ..) cujas soluções (=0) só aparecem quando os coeficientes da equação (a, b, c, …) são inteiros ( … ,-2, -1, 0, 1, 2, … ).

a equação diofantina Linear

uma equação diofantina linear é uma equação do primeiro grau cujas soluções estão restritas aos inteiros. O protótipo linear da equação de Diophantine:

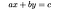
a, onde a, b e c são coeficientes inteiros e x e y são variáveis. Os problemas diofantinos lineares típicos envolvem, portanto, quantidades inteiras, como por exemplo (Brilliant.org, 2019):

How many ways are there to make $2.00 from only nickels and quarters?

As soluções para o problema são encontradas atribuindo variáveis ao número de nickels (x) e ao número de Quartos (y). Sabemos que $ 2 são 200 centavos (c), e que um níquel vale 5 centavos (a) e um quarto 25 centavos (b). Assim, facilmente chegamos à equação especificando o número de maneiras em que podemos ter US $ 2,00 em moedas e moedas:

Agora, porque esta é uma equação com duas incógnitas, nós não podemos resolver para uma variável de cada vez (como se pode fazer com um típico sistema de equações lineares). Em vez disso, para o caso linear, podemos usar o seguinte teorema:

Linear Diophantine equations have integer solutions if and only if c is a multiple of the greatest common divisor of a and b.If integers (x, y) constitute a solution to the linear Diophantine equation for given a, b and c, then the other solutions have the form (x + kv, y - ku) where k is an arbitrary integer and u and v are the quotients of a and b (respectively) by the greatest common divisors of a and b.

O maior divisor comum (MDC) de dois ou mais números inteiros, que não são todos zero, é o maior inteiro positivo que divide cada um dos números inteiros. Para o nosso exemplo acima, podemos começar levando-o divisor comum de 5, obtendo-se:

O maior divisor comum de a e b, de 1 a 5, é de 1. Qualquer c não negativo é um múltiplo de 1. Há nove desses múltiplos de 5 que são menores ou iguais a 40. São 0, 5, 10, 15, 20, 25, 30, 35, 40. Portanto, há nove maneiras de fazer $ 2.00 de moedas e moedas. São:

(0, 8), (5, 7), (10, 6), (15, 5), (20, 4), (25, 3), (30, 2), (35, 1) og (40, 0).

o processo acima é uma versão simples do que é chamado de análise diofantina, o processo necessário para encontrar soluções para equações diofantinas. As perguntas tipicamente feitas durante essas análises são:

• Existem algumas soluções?existem soluções para além de algumas que são facilmente encontradas por inspecção?existem, finitamente ou infinitamente, muitas soluções?todas as soluções podem ser encontradas, em teoria?pode-se, na prática, calcular uma lista completa de soluções?

técnicas populares usadas para resolver equações diofantinas incluem decomposição de fatores, delimitando por desigualdades, parametrização, aritmética modular, indução, descida infinita de Fermat, redução a frações de Pell e contínuas, sistemas numéricos posicionais e curvas elípticas (Wikiversity, 2019).

a equação de Hardy-Ramanujan

o número de Hardy-Ramanujan 1729, conhecido como um “número de táxi” é definido como “o menor número expressável como a soma de dois cubos de duas maneiras diferentes”, de uma anedota do matemático britânico G. H. Hardy when he visited Indian mathematician Srinivasa Ramanujan in the hospital:

“I remember once going to see him when he was ill at Putney. Eu tinha montado no táxi número 1729 e comentou que o número parecia-me bastante aborrecido, e que eu esperava que não era um presságio desfavorável. “Não”, respondeu Ramanujan, ” é um número muito interessante; é o menor número expressável como a soma de dois cubos de duas maneiras diferentes.”- G. H. Hardy (1918)

The equation at the heart of taxicab numbers is Diophantine, namely the equation:

As duas maneiras diferentes de 1729 é poderem ser expressos como a soma de dois cubos são 13 + 123 e 93 + 103. Até agora, seis números de táxis são conhecidos. São:

Ta(1) = 2 
= 1³ + 1³Ta(2) = 1,729 
= 1³ + 12³ = 9³ + 10³Ta(3) = 87,539,319 
= 167³ + 436³ = 228³ + 423³ = 255³ + 414³Ta(4) = 6,963,472,309,248 
= 2421³ + 19083³ = 5436³ + 18948³ = 10200³ + 18072³ = 13322³ + 16630³Ta(5) = 48,988,659,276,962,496
= 38787³ + 365757³ = 107839³ + 362753³ = 205292³ + 342952³ = 221424³ + 336588³ =231518³ + 331954³Ta(6) = 24,153,319,581,254,312,065,344
= 582162³ + 28906206³ = 3064173³ + 28894803³ = 8519281³ + 28657487³ = 16218068³ + 27093208³ = 17492496³ + 26590452³ = 18289922³ + 26224366³

o Último Teorema de Fermat

Números poderem ser expressos como a soma de cubos (tais como aqueles da soma de três cubos problema e o Hardy-Ramanujan número) foram mencionados pela primeira vez em 1657 por Bernard Frénicle de Bessy, que descreveu a propriedade citando o exemplo do número de 1729, em suas correspondências com John Wallis e Pierre de Fermat. Fermat nome pois tornou-se um sinônimo de caso mais geral do problema, seguindo o seu 1637 declaração na margem de uma cópia de Diophantus’ Arithmetica que nenhum de três números inteiros positivos a, b, e c satisfazem a equação de Diophantine

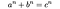
o Que Fermat (em)famosa afirmou que ele havia provado ser verdadeira para valores inteiros de n maior do que 2, mas que ele não poderia incluir em suas notas no livro porque a margem foi de muito estreitas:

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet - Pierre de Fermat, 1637

Traduzido, o texto diz “é impossível para um cubo ser a soma de dois cubos, um quarto poder ser a soma de dois quarto poder, ou, em geral, para qualquer número que é uma potência maior do que o segundo a ser a soma dos dois poderes semelhantes. Descobri uma demonstração verdadeiramente maravilhosa desta proposta de que esta margem é demasiado estreita para conter.”(Nagell, 1951).

a conjectura foi finalmente provada após 358 anos em 1994 pelo matemático inglês Andrew Wiles em seu artigo curvas elípticas modulares e Último Teorema de Fermat publicado nos anais da Matemática 141 (3), pp 443-551. A prova de Wiles por contradição, com 129 páginas de comprimento, usa técnicas da geometria algébrica e da teoria dos números para provar um caso especial do teorema da modularidade para curvas elípticas, que junto com o teorema de Ribet implica a verdade do último teorema de Fermat. Devido ao seu uso extensivo da matemática moderna, é certo que a prova de Wiles não pode ser a mesma reivindicada para ser encontrada por Fermat — que ainda permanece perdida (e provavelmente não foi uma prova em tudo).

triplos pitagóricos

a equação diofantina talvez mais conhecida de todas é um caso particular da equação do Último Teorema de Fermat, mas para n=2. Esta é a equação que ajuda a encontrar o comprimento dos lados de um ângulo direito triângulo

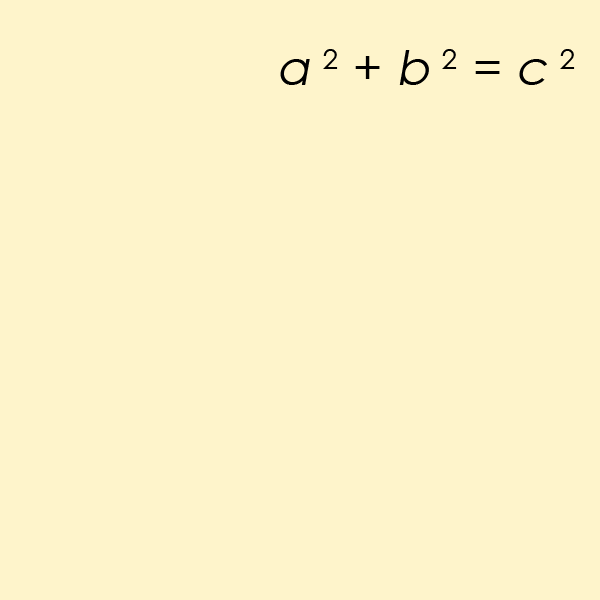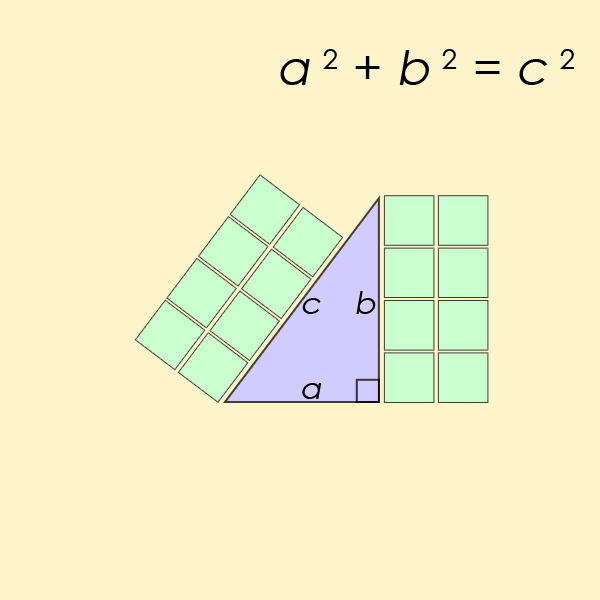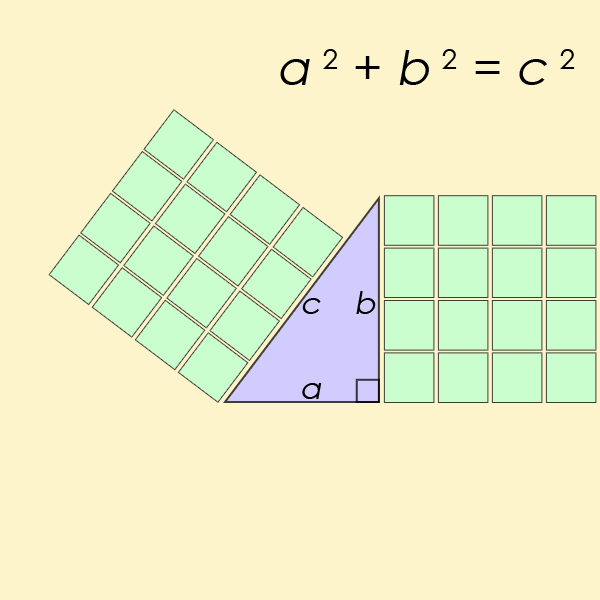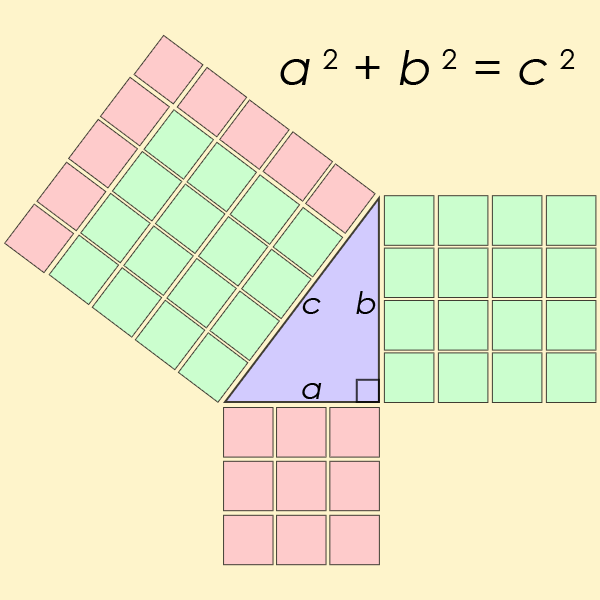
Pell Equação

Pell da equação (às vezes, o Pell-Fermat equação) é toda equação da seguinte forma, onde n é um dado positivo praça livre de número inteiro e inteiro de procura de soluções para x e y:

Esta equação de Diophantine primeiro foi extensivamente estudada pelo matemático Indiano Brahmagupta todo o ano de 628. He developed the so-called chakravala method for solving it and other indeterminate equations. Isto cerca de mil anos antes de seu homônimo, o matemático inglês John Pell (1611-1685) o estudou enquanto trabalhava com Johann Heinrich Rahn. Seu nome surgiu de uma atribuição errada de uma solução fornecida por Lord Brouncker para Pell por Leonard Euler em 1732-33.

Equações da forma de Pell da equação n = 2 são conhecidos têm sido estudadas como início de 400 A.C., na Índia e na Grécia, além disso, para o caso onde x2 − 2y2 = -1, por causa da ligação destas duas equações para o número irracional obtido a partir do cálculo da raiz quadrada de 2 (se x e y são números inteiros positivos satisfazendo esta equação, então x/y é uma aproximação de √2).

em coordenadas cartesianas, a equação tem a forma de uma hipérbole, pois soluções para a equação ocorrem sempre que a curva passa através de um ponto cujas coordenadas x e y são tanto inteiros, como x = 1, y = 0 e x = -1, y = 0. Lagrange provou que enquanto n não é um quadrado perfeito, a equação de Pell tem infinitamente muitas soluções inteiras distintas.

a conjectura de Erdős-Straus

a conjectura de Erdős–Straus afirma que para cada inteiro maior que 2, o número racional 4/n pode ser expresso como a soma de três frações de unidade positivas. Isto é, para cada inteiro n ≥ 2, existem inteiros positivos x,y e z, tais que:

Se n é um número composto (n = pq), em seguida, uma expansão para 4/n pode ser encontrado a partir de uma expansão de 4/p ou 4/p. Assim, se existe um contra-exemplo, o menor n, formando um contra-exemplo teria que ser um número primo. Este resultado está ainda mais restrito a uma das seis progressões aritméticas infinitas modulo 840 (Mordell, 1967).

A conjectura é nomeado após matemáticos Paul Erdős e Ernst G. Straus que formulada em 1948. Continua por provar a partir de 2019. A versão diofantina da equação aparece quando se multiplica pelo denominador em ambos os lados e obtém a sua forma polinomial:

For n=5 for instance, there are two solutions:

Euler’s Sum of Powers Conjecture

Leonard Euler in 1769 incorrectly conjectured that Diophantine equations of the form

That is,

Euler's sum of powers conjecture
For all integers n and k greater than 1, if the sum of the n kth powers of positive integers is itself a kth power, then n is greater than or equal to k.

isto é, que, se a soma dos n primeiros termos de aᵏ é igual a um termo que é em si um kth de energia (e.g. bᵏ), então n deve ser maior que ou igual a k. A conjectura foi uma tentativa de Euler para generalizar o último teorema de Fermat. A conjectura foi refutada em 1966 por Lander e Parkin através de pesquisa por computador, quando descobriram um contra-exemplo para o caso k = 5, anunciado no chamado “shortest paper ever published”:

O caso particular de k = 4 foi posteriormente desmentida por Elkies (1986), que descobriu um método de construção de séries infinitas de counterexamples. O seu menor contra-exemplo foi: