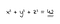
Les équations diophantiennes ont été récemment dans les nouvelles. En effet, le 6 septembre 2019, une équipe dirigée par des chercheurs de l’Université de Bristol et du MIT a annoncé avoir découvert la solution finale au problème dit des « sommes de trois cubes”, qui demande des solutions entières à l’équation x3 + y3 + z3 = k pour des valeurs de k comprises entre 1 et 100. Depuis sa formulation en 1954 à l’Université de Cambridge, jusqu’en 2016, toutes les solutions avaient été trouvées sauf deux, pour k=33 et k=42. En mars de cette année, le mathématicien Andrew R. Booker dans un article publié sur arXiv.org a annoncé qu’il avait trouvé la bonne solution pour k = 33 en utilisant des semaines de temps de calcul sur le supercalculateur de Bristol. Sa solution, présentée dans l’article « Fissurer le problème avec 33” est la suivante:

Puis, il y a une semaine à peine, la nouvelle a de nouveau éclaté: k = 42 avait été découvert, encore une fois par Booker avec un autre Andrew, Andrew Sutherland au MIT, en utilisant le moteur de charité appelé crowd-sourced. Leur réponse est:

Pour des valeurs de k comprises entre 1 et 1000, des solutions restent à trouver pour les entiers 114, 165, 390, 579, 627, 633, 732, 906, 921 et 975.

Le problème des sommes de trois cubes est un exemple de problème demandant des solutions à une équation diophantienne, qui peut être définie comme :

Definition
A Diophantine equation is an algebraic equation with several unknowns and integer coefficients.

Autrement dit, les équations diophantiennes sont des équations comportant plusieurs variables inconnues (x, y, z, ..) dont les solutions (= 0) n’apparaissent que lorsque les coefficients de l’équation (a, b, c, …) sont des entiers ( … ,-2, -1, 0, 1, 2, … ).

L’équation Diophantienne linéaire

Une équation diophantienne linéaire est une équation du premier degré dont les solutions sont limitées à des entiers. L’équation diophantienne linéaire prototypique est :

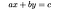
où a, b et c sont des coefficients entiers et x et y sont des variables. Les problèmes diophantiens linéaires typiques impliquent donc des quantités entières, telles que par exemple (Brilliant.org , 2019):

How many ways are there to make $2.00 from only nickels and quarters?

Les solutions au problème sont trouvées en attribuant des variables au nombre de nickels (x) et au nombre de trimestres (y). Nous savons que 2 is, c’est 200 cents (c), et qu’un nickel vaut 5 cents (a) et un quart 25 cents (b). Ainsi, nous arrivons facilement à l’équation spécifiant le nombre de façons dont nous pouvons avoir 2,00 nick en nickels et en trimestres:

Maintenant, comme il s’agit d’une équation unique avec deux inconnues, nous ne pouvons pas résoudre pour une variable à la fois (comme on pourrait le faire avec un système typique d’équations linéaires). Au lieu de cela, pour le cas linéaire, nous pouvons utiliser le théorème suivant:

Linear Diophantine equations have integer solutions if and only if c is a multiple of the greatest common divisor of a and b.If integers (x, y) constitute a solution to the linear Diophantine equation for given a, b and c, then the other solutions have the form (x + kv, y - ku) where k is an arbitrary integer and u and v are the quotients of a and b (respectively) by the greatest common divisors of a and b.

Le plus grand diviseur commun (GCD) de deux entiers ou plus, qui ne sont pas tous nuls, est le plus grand entier positif qui divise chacun des entiers. Pour notre exemple ci-dessus, nous pouvons commencer par factoriser le diviseur commun 5, en obtenant :

Le plus grand diviseur commun de a et b, 1 et 5, est 1. Tout c non négatif est un multiple de 1. Il existe neuf de ces multiples de 5 qui sont inférieurs ou égaux à 40. Ils sont 0, 5, 10, 15, 20, 25, 30, 35, 40. Par conséquent, il existe neuf façons de gagner 2,00 nick à partir de nickels et de quarts. Elles le sont:

(0, 8), (5, 7), (10, 6), (15, 5), (20, 4), (25, 3), (30, 2), (35, 1) og (40, 0).

Le processus ci-dessus est une version simple de ce qu’on appelle l’analyse diophantienne, le processus nécessaire pour trouver des solutions aux équations diophantiennes. Les questions généralement posées lors de ces analyses sont les suivantes :

• Existe-t-il des solutions ?
• Y a-t-il des solutions au-delà de certaines qui sont facilement trouvées par inspection?
• Existe-t-il des solutions infiniment ou infiniment nombreuses ?
• Toutes les solutions peuvent-elles être trouvées, en théorie ?
• Peut-on en pratique calculer une liste complète de solutions ?

Les techniques populaires utilisées pour résoudre les équations diophantiennes comprennent la décomposition des facteurs, la délimitation par inégalités, la paramétrisation, l’arithmétique modulaire, l’induction, la descente infinie de Fermat, la réduction aux fractions de Pell et continues, les systèmes de numération positionnelle et les courbes elliptiques (Wikiversity, 2019).

L’équation de Hardy-Ramanujan

Le nombre de Hardy-Ramanujan 1729, connu sous le nom de « numéro de taxi » est défini comme « le plus petit nombre exprimable comme la somme de deux cubes de deux manières différentes », d’après une anecdote du mathématicien britannique G. H. Hardy quand il a rendu visite au mathématicien indien Srinivasa Ramanujan à l’hôpital:

« Je me souviens d’être allé le voir une fois quand il était malade à Putney. J’avais monté dans le taxi numéro 1729 et remarqué que le numéro me semblait plutôt terne, et que j’espérais que ce n’était pas un présage défavorable. « Non, répondit Ramanujan, c’est un nombre très intéressant ; c’est le plus petit nombre exprimable comme la somme de deux cubes de deux manières différentes.”- G.H. Hardy (1918)

L’équation au cœur des nombres de taxis est diophantienne, à savoir l’équation:

Les deux voies différentes 1729 sont exprimables car la somme de deux cubes est 13 +123 et 93+103. Jusqu’à présent, six numéros de taxi sont connus. Elles le sont:

Ta(1) = 2 
= 1³ + 1³Ta(2) = 1,729 
= 1³ + 12³ = 9³ + 10³Ta(3) = 87,539,319 
= 167³ + 436³ = 228³ + 423³ = 255³ + 414³Ta(4) = 6,963,472,309,248 
= 2421³ + 19083³ = 5436³ + 18948³ = 10200³ + 18072³ = 13322³ + 16630³Ta(5) = 48,988,659,276,962,496
= 38787³ + 365757³ = 107839³ + 362753³ = 205292³ + 342952³ = 221424³ + 336588³ =231518³ + 331954³Ta(6) = 24,153,319,581,254,312,065,344
= 582162³ + 28906206³ = 3064173³ + 28894803³ = 8519281³ + 28657487³ = 16218068³ + 27093208³ = 17492496³ + 26590452³ = 18289922³ + 26224366³

Le dernier théorème de Fermat

Les nombres exprimables comme la somme de cubes (tels que ceux du problème de la somme des trois cubes et du nombre de Hardy-Ramanujan) ont été mentionnés pour la première fois en 1657 par Bernard Frénicle de Bessy, qui a décrit la propriété en citant exemple du numéro 1729 dans ses correspondances avec John Wallis et Pierre de Fermat. Le nom de Fermat est depuis devenu un peu synonyme du cas plus général du problème, à la suite de son affirmation de 1637 dans la marge d’une copie de l’Arithmetica de Diophante selon laquelle trois entiers positifs a, b et c ne satisfont pas l’équation diophantienne

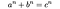
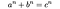
Que Fermat(in) a déclaré qu’il s’était avéré vrai pour des valeurs entières de n supérieures à 2, mais qu’il ne pouvait pas inclure dans ses notes du livre car la marge était trop étroit :

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet - Pierre de Fermat, 1637

Traduit, son texte se lit comme suit : « Il est impossible pour un cube d’être la somme de deux cubes, une quatrième puissance d’être la somme de deux quatrièmes puissances, ou en général pour tout nombre qui est une puissance supérieure à la seconde d’être la somme de deux puissances similaires. J’ai découvert une démonstration vraiment merveilleuse de cette proposition que cette marge est trop étroite pour être contenue. » (Nagell, 1951).

La conjecture a finalement été prouvée après 358 ans en 1994 par le mathématicien anglais Andrew Wiles dans son article Modular elliptic curves and Fermat’s Last Theorem publié dans les Annals of Mathematics 141 (3), pp 443-551. La preuve par contradiction de Wiles, longue de 129 pages, utilise des techniques de la géométrie algébrique et de la théorie des nombres pour prouver un cas particulier du théorème de modularité pour les courbes elliptiques, qui, avec le théorème de Ribet, implique la vérité du dernier théorème de Fermat. En raison de son utilisation intensive des mathématiques modernes, il est certain que la preuve de Wiles ne peut pas être la même que celle que Fermat prétend avoir trouvée — qui reste toujours perdue (et n’était probablement pas du tout une preuve).

Triplets de Pythagore

L’équation diophantienne peut-être la plus connue de toutes est un cas particulier de l’équation du Dernier théorème de Fermat, mais pour n = 2. C’est l’équation qui permet de trouver la longueur des côtés d’un triangle rectangle

>

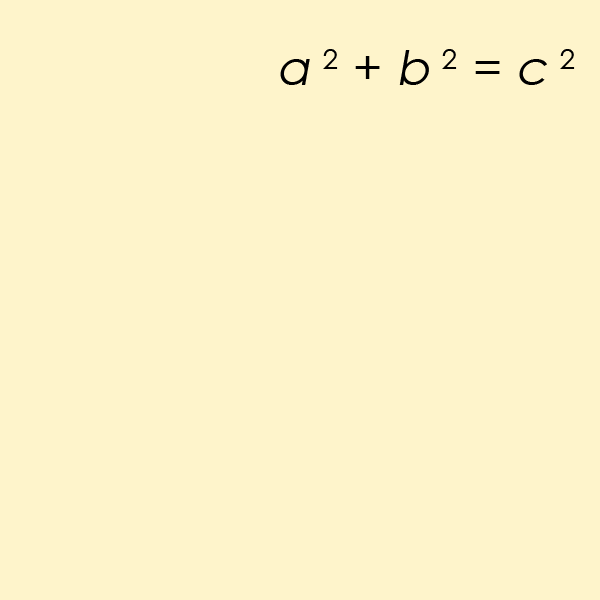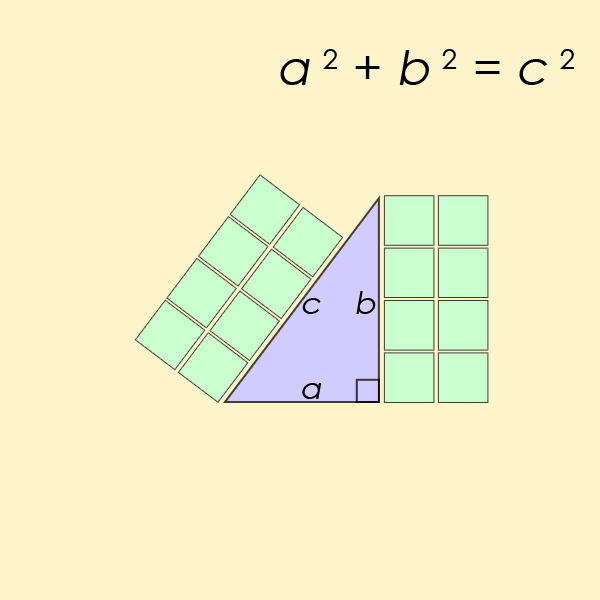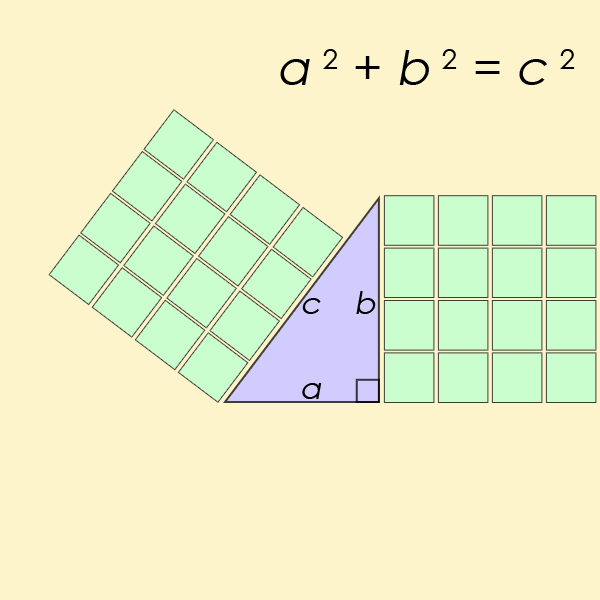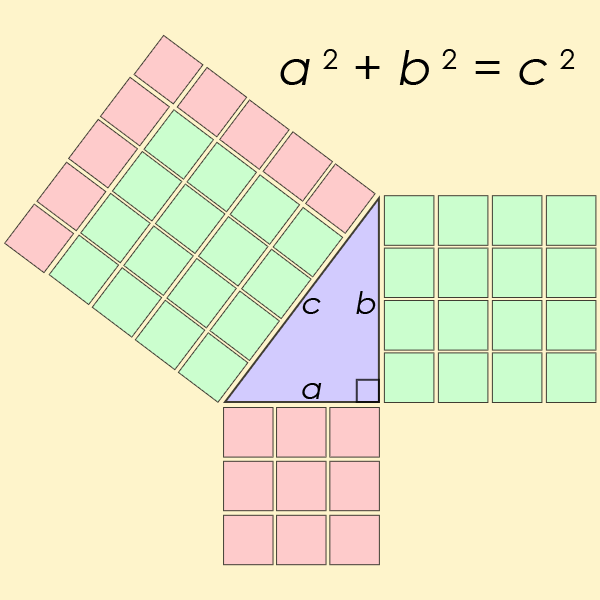
L’équation de Pell

L’équation de Pell (parfois l’équation de Pell-Fermat) est une équation quelconque de la forme suivante où n est un entier sans carré positif donné et des solutions entières sont recherchées pour x et y:

Cette équation diophantienne a été étudiée pour la première fois en profondeur par le mathématicien indien Brahmagupta vers l’an 628. Il a développé la méthode dite de chakravala pour la résoudre et d’autres équations indéterminées. Cela environ mille ans avant son homonyme, le mathématicien anglais John Pell (1611-1685) l’a étudié alors qu’il travaillait sous la direction de Johann Heinrich Rahn. Son nom provient d’une attribution erronée d’une solution fournie par Lord Brouncker à Pell par Leonard Euler en 1732-33.

Des équations de la forme de l’équation de Pell avec n = 2 sont connues pour avoir été étudiées dès 400 av.J.−C. en Inde et en Grèce, en plus du cas où x2-2y2 =-1, en raison de la connexion de ces deux équations au nombre irrationnel obtenu à partir du calcul de la racine carrée de 2 (si x et y sont des entiers positifs satisfaisant cette équation, alors x/y est une approximation de √2).

En coordonnées cartésiennes, l’équation a la forme d’une hyperbole, car les solutions de l’équation se produisent partout où la courbe passe par un point dont les coordonnées x et y sont toutes deux des entiers, tels que x = 1, y = 0 et x =-1, y = 0. Lagrange a prouvé que tant que n n’est pas un carré parfait, l’équation de Pell a une infinité de solutions entières distinctes.

La conjecture d’Erdős–Straus

La conjecture d’Erdős–Straus stipule que pour tout entier supérieur à 2, le nombre rationnel 4/n peut être exprimé comme la somme de trois fractions unitaires positives. Autrement dit, pour chaque entier n ≥ 2, il existe des entiers positifs x, y et z tels que :

div>

Si n est un nombre composite (n = pq), alors une expansion pour 4 / n pourrait être trouvée à partir d’une expansion de 4 / p ou 4 / q. Ainsi, si un contre-exemple existe, le plus petit n formant un contre-exemple devrait être un nombre premier. Ce résultat sera encore limité à l’une des six progressions arithmétiques infinies modulo 840 (Mordell, 1967).

La conjecture porte le nom des mathématiciens Paul Erdős et Ernst G. Straus qui l’ont formulée en 1948. Il reste non prouvé en 2019. La version diophantienne de l’équation apparaît lorsque l’on multiplie par le dénominateur des deux côtés et obtient sa forme polynomiale:

For n=5 for instance, there are two solutions:

Euler’s Sum of Powers Conjecture

Leonard Euler in 1769 incorrectly conjectured that Diophantine equations of the form

That is,

Euler's sum of powers conjecture
For all integers n and k greater than 1, if the sum of the n kth powers of positive integers is itself a kth power, then n is greater than or equal to k.

C’est-à-dire que si la somme des n premiers termes de a is est égale à un terme qui est lui-même une kème puissance (par exemple bᵏ), alors n doit être supérieur ou égal à k. La conjecture était une tentative d’Euler de généraliser le dernier théorème de Fermat. La conjecture a été réfutée en 1966 par Lander et Parkin grâce à une recherche informatique, lorsqu’ils ont découvert un contre-exemple pour le cas k = 5, annoncé dans le soi-disant « article le plus court jamais publié”.:

Le cas particulier de k = 4 a ensuite été réfuté par Elkies (1986) qui a découvert une méthode de construction de séries infinies de contre-exemples. Son plus petit contre-exemple était :