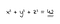
equazioni Diofantee sono stato nelle notizie ultimamente. Questo perché, il 6 settembre 2019 un team guidato da ricercatori dell’Università di Bristol e del MIT ha annunciato di aver scoperto la soluzione finale al cosiddetto problema “somme di tre cubi”, che chiede soluzioni intere all’equazione x3 + y3 + z3 = k per valori di k compresi tra 1 e 100. Dalla sua formulazione nel 1954 presso l’Università di Cambridge, fino al 2016, ogni soluzione era stata trovata tranne due, per k=33 e k=42. Nel marzo di quest’anno, il matematico Andrew R. Booker in un articolo pubblicato su arXiv.org ha annunciato di aver trovato la soluzione corretta per k=33 usando settimane di tempo di calcolo sul supercomputer di Bristol. La sua soluzione, presentata nel libro “spezzare il problema con 33” è:

Poi, appena una settimana fa, la di nuovo la notizia: k=42 era stato scoperto, sempre da parte di Booker con un altro Andrew, Andrew Sutherland al MIT, utilizzando il crowd-sourced cosiddetta Carità Motore. La loro risposta è:

Per i valori di k tra 1 e 1000, soluzioni restano ancora da trovare per i numeri interi 114, 165, 390, 579, 627, 633, 732, 906, 921 e 975.

Il problema delle somme di tre cubi è un esempio di un problema che chiede soluzioni a un’equazione diofantina, che può essere definita come:

Definition
A Diophantine equation is an algebraic equation with several unknowns and integer coefficients.

Cioè, le equazioni diofantee sono equazioni con diverse variabili sconosciute (x,y, z, ..) le cui soluzioni (=0) appaiono solo quando i coefficienti dell’equazione (a, b, c,,) sono interi ( … ,-2, -1, 0, 1, 2, … ).

L’equazione diofantina lineare

Un’equazione diofantina lineare è un’equazione di primo grado le cui soluzioni sono limitate agli interi. Il prototipo Diofantee lineari equazione è:

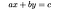
in cui un, b e c sono coefficienti interi x e y sono variabili. I tipici problemi diofantini lineari coinvolgono quindi quantità intere, come ad esempio (Brilliant.org, 2019):

How many ways are there to make $2.00 from only nickels and quarters?

Le soluzioni al problema si trovano assegnando variabili al numero di nickel (x) e al numero di quarti (y). Sappiamo che $2 è 200 centesimi (c), e che un nichel vale 5 centesimi (a) e un quarto 25 centesimi (b). Quindi, arriviamo facilmente all’equazione che specifica il numero di modi in cui possiamo avere $2.00 in nichelini e quarti:

Ora, perché questa è una singola equazione con due incognite, siamo in grado di risolvere per una variabile alla volta, come si potrebbe fare con un tipico sistema di equazioni lineari). Invece, per il caso lineare, possiamo usare il seguente teorema:

Linear Diophantine equations have integer solutions if and only if c is a multiple of the greatest common divisor of a and b.If integers (x, y) constitute a solution to the linear Diophantine equation for given a, b and c, then the other solutions have the form (x + kv, y - ku) where k is an arbitrary integer and u and v are the quotients of a and b (respectively) by the greatest common divisors of a and b.

Il massimo comun divisore (GCD) di due o più interi, che non sono tutti zero, è il più grande numero intero positivo che divide ciascuno degli interi. Per il nostro esempio precedente, possiamo cominciare da escludere comune divisore 5, ottenendo:

Il più grande divisore comune di a e b, 1 e 5, è 1. Qualsiasi c non negativo è un multiplo di 1. Ci sono nove multipli di 5 che sono inferiori o uguali a 40. Lo sono 0, 5, 10, 15, 20, 25, 30, 35, 40. Pertanto, ci sono nove modi per fare $2.00 da nichelini e quarti. Loro sono:

(0, 8), (5, 7), (10, 6), (15, 5), (20, 4), (25, 3), (30, 2), (35, 1) og (40, 0).

Il processo di cui sopra è una versione semplice di quella che viene chiamata analisi diofantina, il processo richiesto per trovare soluzioni alle equazioni diofantee. Le domande poste tipicamente durante tali analisi sono:

• Ci sono soluzioni?
• Ci sono soluzioni oltre ad alcune che sono facilmente reperibili mediante ispezione?
• Ci sono finitamente o infinitamente molte soluzioni?
• Tutte le soluzioni possono essere trovate, in teoria?
• Si può in pratica calcolare un elenco completo di soluzioni?

Le tecniche popolari utilizzate per risolvere equazioni diofantee includono la decomposizione dei fattori, delimitazione per disuguaglianze, parametrizzazione, aritmetica modulare, induzione, discesa infinita di Fermat, riduzione alle frazioni di Pell e continue, sistemi numerali posizionali e curve ellittiche (Wikiversity, 2019).

L’equazione di Hardy-Ramanujan

Il numero di Hardy-Ramanujan 1729, noto come “numero di taxi cab” è definito come “il più piccolo numero esprimibile come somma di due cubi in due modi diversi”, da un aneddoto del matematico britannico G. H. Hardy quando visitò il matematico indiano Srinivasa Ramanujan in ospedale:

“Ricordo che una volta andai a trovarlo quando era malato a Putney. Avevo guidato in taxi numero 1729 e ha osservato che il numero mi sembrava piuttosto un noioso, e che speravo che non era un presagio sfavorevole. ” No”, rispose Ramanujan, ” è un numero molto interessante; è il numero più piccolo esprimibile come somma di due cubi in due modi diversi.”- G. H. Hardy (1918)

L’equazione al centro dei numeri di taxi è diofantina, vale a dire l’equazione:

I due diversi modi 1729 è esprimibile come somma di due cubi sono 13 + 123 e 93 + 103. Finora sono noti sei numeri di taxi. Loro sono:

Ta(1) = 2 
= 1³ + 1³Ta(2) = 1,729 
= 1³ + 12³ = 9³ + 10³Ta(3) = 87,539,319 
= 167³ + 436³ = 228³ + 423³ = 255³ + 414³Ta(4) = 6,963,472,309,248 
= 2421³ + 19083³ = 5436³ + 18948³ = 10200³ + 18072³ = 13322³ + 16630³Ta(5) = 48,988,659,276,962,496
= 38787³ + 365757³ = 107839³ + 362753³ = 205292³ + 342952³ = 221424³ + 336588³ =231518³ + 331954³Ta(6) = 24,153,319,581,254,312,065,344
= 582162³ + 28906206³ = 3064173³ + 28894803³ = 8519281³ + 28657487³ = 16218068³ + 27093208³ = 17492496³ + 26590452³ = 18289922³ + 26224366³

l’Ultimo Teorema di Fermat

Numeri rappresentabili come somma di cubi (come quelli dalla somma di tre cubi problema e di Hardy-Ramanujan numero) sono state per la prima volta menzionato nel 1657 da Bernard Frénicle de Bessy, che ha descritto le proprietà citando l’esempio del numero 1729 nella sua corrispondenza con John Wallis e Pierre de Fermat. Fermat nome dal momento che è diventato sinonimo con il caso più generale del problema, seguendo il suo 1637 affermazione a margine di una copia di Diophantus’ Arithmetica che non tre numeri interi positivi a, b, e c soddisfano l’equazione Diofantea

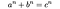
Che Fermat (in)notoriamente dichiarato che aveva dimostrato di essere la vera per i valori interi di n maggiore di 2, ma che egli non poteva includere nelle sue note nel libro perché il margine di too narrow:

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet - Pierre de Fermat, 1637

Tradotto, il suo testo recita “È impossibile che un cubo sia la somma di due cubi, una quarta potenza sia la somma di due quarta potenza, o in generale per qualsiasi numero che sia una potenza maggiore della seconda sia la somma di due potenze simili. Ho scoperto una dimostrazione davvero meravigliosa di questa proposta che questo margine è troppo stretto per contenere.”(Nagell, 1951).

La congettura è stata notoriamente finalmente dimostrata dopo 358 anni nel 1994 dal matematico inglese Andrew Wiles nel suo articolo Modular elliptic curves and Fermat’s Last Theorem pubblicato negli Annals of Mathematics 141 (3), pp 443-551. La dimostrazione di Wiles per contraddizione, lunga 129 pagine, utilizza tecniche di geometria algebrica e teoria dei numeri per dimostrare un caso speciale del teorema di modularità per le curve ellittiche, che insieme al teorema di Ribet implica la verità dell’ultimo teorema di Fermat. A causa del suo ampio uso della matematica moderna, è certo che la prova di Wiles non può essere la stessa che si afferma essere stata trovata da Fermat — che rimane ancora persa (e probabilmente non era affatto una prova).

Tripli pitagorici

L’equazione diofantina forse più nota di tutte è un caso particolare dell’equazione dell’ultimo Teorema di Fermat, ma per n=2. Questa è l’equazione che aiuta a trovare la lunghezza dei lati di un ad angolo retto del triangolo

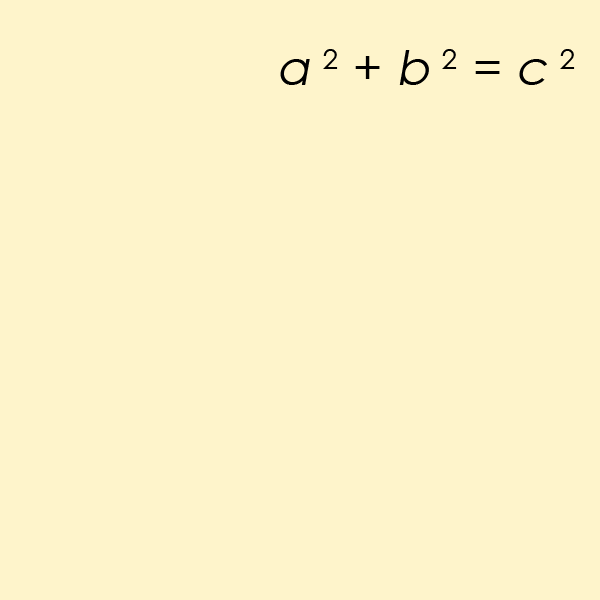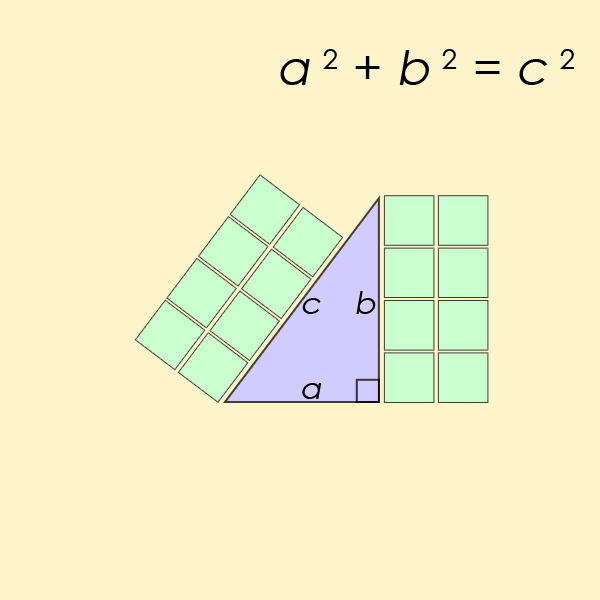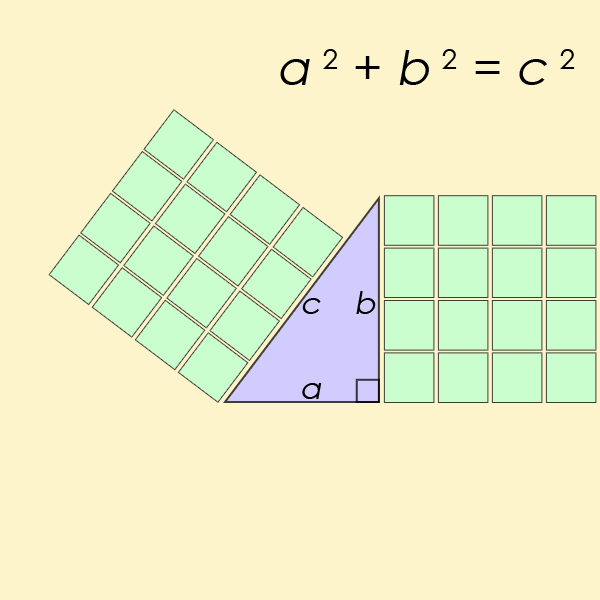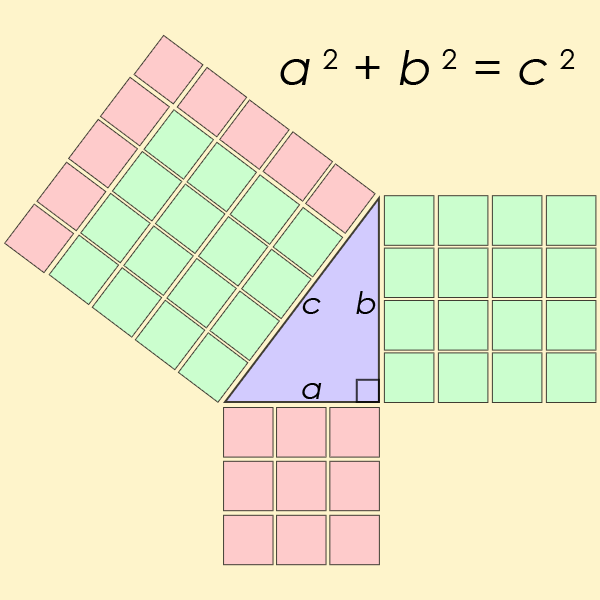
L’equazione di Pell

L’equazione di Pell (a volte l’equazione di Pell-Fermat) è una qualsiasi equazione della seguente forma in cui n è un dato numero intero positivo privo di quadrati e le soluzioni intere sono ricercate per x e y:

Questa equazione Diofantea è stato prima studiato ampiamente dal matematico Indiano Brahmagupta intorno all’anno 628. Ha sviluppato il cosiddetto metodo chakravala per risolverlo e altre equazioni indeterminate. Questo circa mille anni prima del suo omonimo, il matematico inglese John Pell (1611-1685) lo studiò mentre lavorava sotto Johann Heinrich Rahn. Il suo nome deriva da un’errata attribuzione di una soluzione fornita da Lord Brouncker a Pell da Leonard Euler nel 1732-33.

Equazioni della forma dell’equazione di Pell con n = 2, sono stati studiati come già 400 A.C. in India e Grecia, oltre che per il caso in cui x2 − 2y2 = -1, a causa della connessione di queste due equazioni, il numero irrazionale ottenuto dal calcolo della radice quadrata di 2 (se x e y sono numeri interi positivi che soddisfano tale equazione, allora x/y è un’approssimazione di √2).

In coordinate cartesiane, l’equazione ha la forma di un’iperbole, poiché le soluzioni all’equazione si verificano ovunque la curva passi attraverso un punto le cui coordinate x e y sono entrambe numeri interi, come x = 1, y = 0 e x = -1, y = 0. Lagrange ha dimostrato che finché n non è un quadrato perfetto, l’equazione di Pell ha infinite soluzioni intere distinte.

La congettura di Erdős–Straus

La congettura di Erdős–Straus afferma che per ogni intero maggiore di 2, il numero razionale 4/n può essere espresso come somma di tre frazioni unitarie positive. Che, per ogni intero n ≥ 2, esiste interi positivi x,y e z tali che:

Se n è un composito numero (n = pq), quindi un’espansione per 4/n potrebbe essere trovato da un espansione di 4/p, 4/q. Così, se un controesempio esiste, il più piccolo n formando un controesempio dovrebbe essere un numero primo. Questo risultato è ulteriormente limitato a una delle sei progressioni aritmetiche infinite modulo 840 (Mordell, 1967).

La congettura è chiamato dopo i matematici Paul Erdős e Ernst G. Straus che ha formulato nel 1948. Rimane non provato a partire dal 2019. La versione diofantina dell’equazione appare quando si moltiplica per il denominatore su entrambi i lati e ottiene la sua forma polinomiale:

For n=5 for instance, there are two solutions:

Euler’s Sum of Powers Conjecture

Leonard Euler in 1769 incorrectly conjectured that Diophantine equations of the form

That is,

Euler's sum of powers conjecture
For all integers n and k greater than 1, if the sum of the n kth powers of positive integers is itself a kth power, then n is greater than or equal to k.

Cioè, se la somma dei primi n termini di Aᵏ è uguale a un termine che è esso stesso una potenza kth (ad esempio b b), allora n deve essere maggiore o uguale a k. La congettura era un tentativo di Eulero di generalizzare l’ultimo teorema di Fermat. La congettura fu smentita nel 1966 da Lander e Parkin attraverso la ricerca al computer, quando scoprirono un controesempio per il caso k=5, annunciato nel cosiddetto “documento più breve mai pubblicato”:

Il caso speciale di k = 4 fu successivamente smentito da Elkies (1986) che scoprì un metodo per costruire serie infinite di controesempi. Il suo più piccolo controesempio era: